Four charges equal to -Q are placed at the four corners of a square and a charge q is at its centre. If the system is in equilibrium, the value of q is

• $\frac{-\mathrm{Q}}{4}\left(1 + 2\sqrt{2}\right)$

• $\frac{\mathrm{Q}}{4}\left(1 + 2\sqrt{2}\right)$

• $\frac{-\mathrm{Q}}{2}\left(1 + 2\sqrt{2}\right)$

• $\frac{\mathrm{Q}}{2}\left(1 + 2\sqrt{2}\right)$

192.

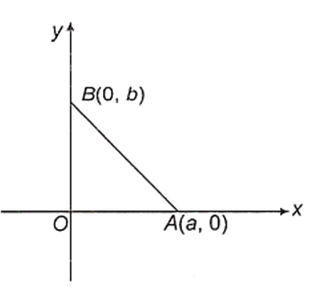
A charge +q is placed at the origin O of x-y axes as shown in the figure. The work done in taking a charge Q from A to B along the straight line AB is

     

• $\frac{\mathrm{qQ}}{4{\mathrm{\pi \epsilon }}_0}\left(\frac{\mathrm{a} - \mathrm{b}}{\mathrm{ab}}\right)$

• $\frac{\mathrm{qQ}}{4{\mathrm{\pi \epsilon }}_0}\left(\frac{\mathrm{b} - \mathrm{a}}{\mathrm{ab}}\right)$

• $\frac{\mathrm{qQ}}{4{\mathrm{\pi \epsilon }}_0}\left(\frac{\mathrm{b}}{{\mathrm{a}}^2} - \frac{1}{\mathrm{b}}\right)$

• $\frac{\mathrm{qQ}}{4{\mathrm{\pi \epsilon }}_0}\left(\frac{\mathrm{a}}{{\mathrm{b}}^2} - \frac{1}{\mathrm{b}}\right)$

In a region, the intensity of an electric field is given by E = 2i + 3j+ k in Nc^-1. The electric flux through a surface S = 1Oi m² in the region is

• 5 Nm²C^-1

• 10 Nm²C^-1

• 15 Nm²C^-1

• 20 Nm²C^-1

Two infinite parallel metal planes, contain electric charges with charge densities +σ and -σ respectively and they are separated by a small distance in air. If the permittivity of air is ε₀,then the magnitude of the field between the two planes with its direction will be

• σ/ε₀ towards the positively charged plane

• σ/ε₀ towards the negatively charged plane

• σ/(2ε₀) towards the positively charged plane

• 0 and towards any direction

Two pith balls carrying equal charges are suspended from a common point by strings of equal length, the equilibrium separation between them is r. Now the strings are rigidly clamped at half the height. The equilibrium separation between the balls now become

• ${\left(\frac{1}{\sqrt{2}}\right)}^2$

• $\left(\frac{\mathrm{r}}{\sqrt[3]{2}}\right)$

• $\left(\frac{2\mathrm{r}}{\sqrt{3}}\right)$

• $\left(\frac{2\mathrm{r}}{3}\right)$

An infinite sheet carrying a uniform surface charge density σ lies on the xy-plane. The work done to carry a charge q from the point $\mathrm{A} = \mathrm{a}(\hat{\mathrm{i}} + 2\hat{\mathrm{j}} + 3\hat{\mathrm{k}})$ to the point $\mathrm{B}\hspace{0.17em}= \mathrm{a}(\hat{\mathrm{i}} - 2\hat{\mathrm{j}} + 6\hat{\mathrm{k}})$ (where a is a constant with the dimension of length and ε₀ is the permittivity of free space) is

• $\frac{3\mathrm{\sigma aq}}{2{\mathrm{\epsilon }}_0}$

• $\frac{2\mathrm{\sigma aq}}{{\mathrm{\epsilon }}_0}$

• $\frac{5\mathrm{\sigma aq}}{2{\mathrm{\epsilon }}_0}$

• $\frac{3\mathrm{\sigma aq}}{{\mathrm{\epsilon }}_0}$

Consider two concentric spherical metal shells of radii r₁ and r₂ (r₂ > r₁). If the outer shell has a charge q and the inner one is grounded, the charge on the inner shell is

• $\frac{- {\mathrm{r}}_2}{{\mathrm{r}}_1} \mathrm{q}$

• zero

• $\frac{- {\mathrm{r}}_1}{{\mathrm{r}}_2} \mathrm{q}$

• - q

The line AA' is on charged infinite conducting plane which is perpendicular to the plane of the of the paper. The plane has a surface density of charge σ and B is ball of mass m with a like charge of magnitude q. B is connected by string from a point on the line AA'. The tangent of angle (θ) formed between the line AA' and the string is

• $\frac{\mathrm{q\sigma }}{2{\mathrm{\epsilon }}_0\mathrm{mg}}$

• $\frac{\mathrm{q\sigma }}{4{\mathrm{\pi \epsilon }}_0\mathrm{mg}}$

• $\frac{\mathrm{q\sigma }}{2{\mathrm{\pi \epsilon }}_0\mathrm{mg}}$

• $\frac{\mathrm{q\sigma }}{{\mathrm{\epsilon }}_0\mathrm{mg}}$

A hollow sphere of external radius R and thickness (t << R) is made of a metal of density ρ. The sphere will float in water, if

• $\mathrm{t} \le \frac{\mathrm{R}}{\mathrm{\rho }}$

• $\mathrm{t} \le \frac{\mathrm{R}}{3\mathrm{\rho }}$

• $\mathrm{t} \le \frac{\mathrm{R}}{2\mathrm{\rho }}$

• $\mathrm{t} \ge \frac{\mathrm{R}}{3\mathrm{\rho }}$

A charge q is placed at one corner of a cube. The electric flux through any of the three faces adjacent to the charge is zero. The flux through any one of the other three faces is

• q/3ε₀

• q/6ε₀

• q/12ε₀

• q/24ε₀