The magnetic dipole moment of a current loop is independent of

• magnetic field in which it is lying

• number of turns

• area of the loop

• current in the loop

Magnetic field at the centre of a circular coil of radius R due to i flowing through it is B. The magnetic field at a point along the axis at distance R from the centre is

• $\frac{\mathrm{B}}{2}$

• $\frac{\mathrm{B}}{4}$

• $\frac{\mathrm{B}}{\sqrt{8}}$

• $\sqrt{8}\mathrm{B}$

Two thick wires and two thin wires, all of same material and same length, form a square in three different ways P, Q and R as shown in the figure. With correct connections shown, the magnetic field due to the current flow, at the centre of the loop will be zero in case of

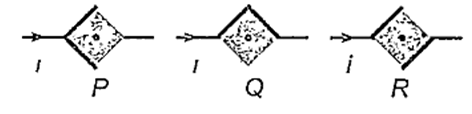
• Q and R

• P only

• P and Q

• P and R

There is a uniform magnetic field directed perpendicular and into the plane of the paper. An irregular shaped conducting loop is slowly changing into a circular loop in the plane of the paper. Then

• current is induced in the loop in the anticlockwise direction

• current is induced in the loop in the clockwise direction

• AC is induced in the loop

• no current is induced in the loop

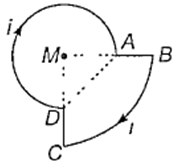
A current i is flowing through the loop. The direction of the current and the shape of the loop are as shown in the figure. The magnetic field at the centre of the loop is $\frac{{\mathrm{\mu }}_0\mathrm{i}}{\mathrm{R}}$ times (MA = R, MB = 2R, $\angle \mathrm{DMA} = 90°$

• $\frac{5}{16}, \mathrm{but} \mathrm{out} \mathrm{of} \mathrm{the} \mathrm{plane} \mathrm{of} \mathrm{the} \mathrm{paper}$

• $\frac{5}{16}, \mathrm{but} \mathrm{into} \mathrm{the} \mathrm{plane} \mathrm{of} \mathrm{the} \mathrm{paper}$

• $\frac{7}{16}, \mathrm{but} \mathrm{out} \mathrm{of} \mathrm{the} \mathrm{plane} \mathrm{of} \mathrm{the} \mathrm{paper}$

• $\frac{7}{16}, \mathrm{but} \mathrm{into} \mathrm{the} \mathrm{plane} \mathrm{of} \mathrm{the} \mathrm{paper}$

PQ and RS are long parallel conductors separated by certain distance. M is the midpoint between them (see the figure). The net magnetic field M is B. Now, the current 2 A is switched off. The field at M now becomes

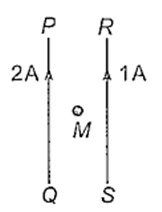
• 2B

• B

• $\frac{\mathrm{B}}{2}$

• 3B

An electron enters the space between the plates of a charged capacitor as shown. The charge density on the plate is σ. Electric intensity in the space between the plates is E. A uniform magnetic field B also exists in the space perpendicular to the direction of E. The electron moves perpendicular to both $\overrightarrow{\mathrm{E}}$ and $\overrightarrow{\mathrm{B}}$ without any change in direction. The time taken by the electron to travel a distance l in the space is

• $\frac{\mathrm{\sigma l}}{{\mathrm{\epsilon }}_0\mathrm{B}}$

• $\frac{\mathrm{\sigma B}}{{\mathrm{\epsilon }}_0\mathrm{l}}$

• $\frac{{\mathrm{\epsilon }}_0\mathrm{lB}}{\mathrm{\sigma }}$

• $\frac{{\mathrm{\epsilon }}_0\mathrm{l}}{\mathrm{\sigma B}}$

A charge +Q is moving upwards vertically. It enters a magnetic field directed to north. The force on the charge will be towards

• north

• south

• east

• west

129.

The torque required to hold a small circular coil of 10 turns, area 1 mm² and carrying a current of $\left(\frac{21}{44}\right)$ A in the middle of a long solenoid of 10³ turns/m carrying a current of 2.5 A, with its axis perpendicular to the axis of the solenoid is

               

• 1.5 × 10^-6 N-m

• 1.5 × 10^-8 N-m

• 1.5 × 10⁺⁶ N-m

• 1.5 × 10⁺⁸ N-m

A particle of charge e and mass m moves with a velocity v in a magnetic field B applied perpendicular to the motion of the particle. The radius r of its path in the field is

• $\frac{\mathrm{mv}}{\mathrm{Be}}$

• $\frac{\mathrm{Be}}{\mathrm{mv}}$

• $\frac{\mathrm{ev}}{\mathrm{Bm}}$

• $\frac{\mathrm{Bv}}{\mathrm{em}}$