The magnetic field at the centre of a current carrying loop of radius 0.1 m is $5\sqrt{5}$ times that at a point along its axis. The distance of this point from the centre of the loop is

• 0.1 m

• 0.2 m

• 0.05 m

• 0.25 m

A wire carrying currenti is shaped as shown. Section AB is a quarter circle of radius r. The magnetic field is directed

• perpendicular to the plane of the paper and directed into the paper

• at an angle $\frac{\mathrm{\pi }}{4}$to the plane of the paper

• along the bisector of the angle ACB away from AB

• along the bisector of ACB towards AB

The wire loop formed by joining two semicircular sections of radii R₁ and R₂ and centre C, carries a current I as shown. The magnetic field at C has a magnitude

• $\frac{{\mathrm{\mu }}_0\mathrm{I}}{2} \left(\frac{1}{{\mathrm{R}}_1} - \frac{1}{{\mathrm{R}}_2}\right)$

• $\frac{{\mathrm{\mu }}_0\mathrm{I}}{4} \left(\frac{1}{{\mathrm{R}}_1} - \frac{1}{{\mathrm{R}}_2}\right)$

• $\frac{{\mathrm{\mu }}_0\mathrm{I}}{2} \left(\frac{1}{{\mathrm{R}}_1} + \frac{1}{{\mathrm{R}}_2}\right)$

• $\frac{{\mathrm{\mu }}_0\mathrm{I}}{4} \left(\frac{1}{{\mathrm{R}}_1} + \frac{1}{{\mathrm{R}}_2}\right)$

A particle of unit mass and specific charge s is thrown from the wall perpendicularly to a wall at a distance d from the wall with speed 'v'. The minimum magnetic field produced so that the particle does not touch the wall, is:

• $\frac{\mathrm{v}}{\mathrm{sd}}$

• $\frac{2\mathrm{v}}{\mathrm{sd}}$

• $\frac{\mathrm{v}}{2\mathrm{sd}}$

• $\frac{\mathrm{v}}{4\mathrm{sd}}$

165.

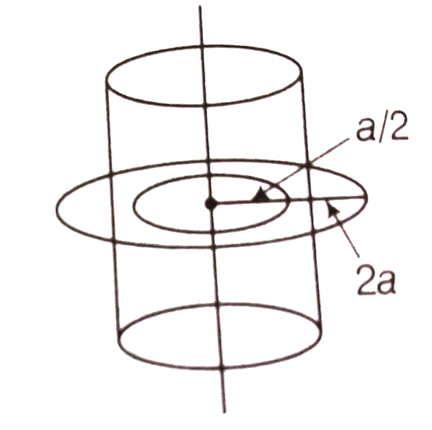
A long straight wire of radius a carries a steady current I. The current is uniformly distributed over its cross-section. The ratio of the magnetic fields B and B' at radial distances 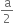 and 2a respectively, from the axis of the wire is,

• 

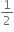
• 1

• 4

• 4

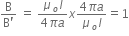
A magnetic needle suspended parallel to a magnetic field requires 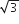 J of work to turn it through  60^o. The torque needed to maintain the needle in this position will be

• 

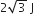
• 3 J

• 
• 

The ratio of amplitude of magnetic field to the amplitude of electric field for an electromagnetic wave propagating in vacuum is equal to

• the speed of light in vacuum

• the reciprocal of the speed of light in vacuum

• the ratio of magnetic permeability to the electric susceptibility of vacuum

• the ratio of magnetic permeability to the electric susceptibility of vacuum

Two similar coils of radius R are lying concentrically with their planes at right angles to each other. The currents flowing in them are I and 2I, respectively. The resultant magnetic field induction at the centre will be

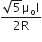
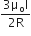
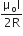
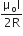
An electric dipole of moment p is placed in an electric field of intensity E. The dipole acquires a position such that the axis of the dipole makes an angle θ with the direction of the field. Assuming that the potential energy of the dipole to be zero when θ =90^o, the torque and the potential energy of the dipole will respectively be

• pE sin θ, pE cos θ

• pE sin θ,-2pE cos θ

• pE sin θ, 2 pE cos θ

• pE sin θ, 2 pE cos θ

A wire loop is rotated in a magnetic field. The frequency of change of direction of the induced emf is

• one per revolution

• twice per revolution

• four times per revolution

• four times per revolution