The activity of a radioactive sample is measured as N_o counts per minute at t = 0 and N_o/e counts per minute at t = 5 min. The time (in minute) at which the activity reduces to half its value is

• log_e 2 /5

• 5/ log_e 2

• 5 log₁₀ 2

• 5 log₁₀ 2

The decay constant of a ratio isotope is λ. If A₁ and A₂ are its activities at times t₁ and t₂ respectively, te number of nuclei which have decayed during the time (t₁-t₂)

• A₁t₁ - A₂t₂

• A₁ - A₂

• (A₁ - A₂)/λ

• (A₁ - A₂)/λ

The binding energy per nucleon in deuterium and helium nuclei are 1.1 MeV and 7.0 MeV, respectively. When two deuterium nuclei fuse to form a helium nucleus the energy released in the fusion is

• 23.6 MeV

• 2.2 MeV

• 28.0 MeV

• 28.0 MeV

In the nuclear decay given below,


the particle emitted in the sequence are

• β, α, γ

• γ, β, α, 

•  β,γ, α

•  β,γ, α

The number of beta particles emitted by radioactive substance is twice the number  of alpha particle emitted by it. The resulting daughter is an 

• isobar of parent

• isomer of parent

• isotone of parent

• isotone of parent

Two radioactive materials X₁ and X₂ have decay constant 5 λ respectively. If initially, they have the same number of nuclei, then the ratio of the number of nuclei of X₁ to that of X₂ will be 1/e after a time

• λ

• λ/2

• 1/4λ

• 1/4λ

147.

If M (A, Z), M_P and M_n denote the masses of the nucleus   proton and neutron respectively in units of u (1 u = 931.5 MeV/c²) and BE represents its binding energy  in MeV, then

• M (A,Z) = ZM_p + (A-Z)M_n - BE/c²

• M (A,Z) = ZM_p + (A-Z)M_n + BE

• M (A,Z) = ZM_p + (A-Z)M_n - BF

• M (A,Z) = ZM_p + (A-Z)M_n - BF

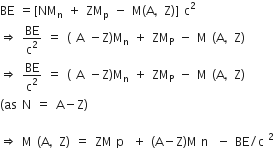
Two nuclei have their mass number in the ratio of 1:3. The ratio of their nuclear densities would be

• 1:3

• 3:1

• (3)^1/3 : 1

• (3)^1/3 : 1

In radioactive decay process, the negatively charged emitted beta particles are:

• the electrons present inside the nucleus

• the electrons produced as a result  of the decay of neutrons inside the nucleus

• the electrons produced as a result of collisions between atoms

• the electrons produced as a result of collisions between atoms

A nucleus has  mass represented by  M (A, Z). If M_p and M_n denote the mass of proton and neutron respectively and BE the binding energy (in MeV), then:

• BE = [M(A,Z)-ZM_p - (A-Z)M_n]c²

• BE = [ZM_p + (A-Z)M_n -M(A,Z)]c²

• BE = [ZM_p + AM_n - M (A,Z)]c²

• BE = [ZM_p + AM_n - M (A,Z)]c²