The total energy of particle, executing simple harmonic motion is

• ∝ x

• ∝ x²

• independent of x

• independent of x

A particle of mass m is attached to a spring (of spring constant k) and has a natural angular frequency ω₀. An external force F(t) proportional to cosωt (ω≠ω₀) is applied to the oscillator. The time displacement of the oscillator will be proportional to

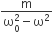
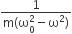
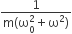
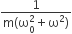
In forced oscillation of a particle the amplitude is maximum for a frequency ω₁ of the force, while the energy is maximum for a frequency ω₂ of the force, then

• ω₁ = ω₂

• ω₁ > ω₂

• ω₁ < ω₂ when damping is small and ω₁ > ω₂ when damping is large

• ω₁ < ω₂ when damping is small and ω₁ > ω₂ when damping is large

A massless spring of length l and spring constant k is placed vertically on a table. A ball of mass m is just kept on top of the spring. The maximum velocity of the ball is

• $\mathrm{g}\sqrt{\frac{\mathrm{m}}{\mathrm{k}}}$

• $\mathrm{g}\sqrt{\frac{2\mathrm{m}}{\mathrm{k}}}$

• $2\mathrm{g}\sqrt{\frac{\mathrm{m}}{\mathrm{k}}}$

• $\frac{\mathrm{g}}{2} \sqrt{\frac{\mathrm{m}}{\mathrm{k}}}$

35.

A particle of mass 3 kg, attached to a spring with force constant 48 N/m execute simple harmonic motion on a frictionless horizontal surface. The time period of oscillation of the particle, in seconds, is

• $\mathrm{\pi }/4$

• $\mathrm{\pi }/2$

• $2\mathrm{\pi }$

• $8\mathrm{\pi }$

The position and velocity of a particle executing simple harmonic motion at t = 0 are given by 3 cm/s and 8 cm/s respectively. If the angular frequency of the particle is 2 rad/s, then the amplitude of oscillation, in centimeters, is

• 3

• 4

• 5

• 6

A simple harmonic motion is represented by x(t) = sin² ωt − 2 cos² ωt. The angular frequency of oscillation is given by

• ω

• 2ω

• 4ω

• ω/2

Two equal masses hung from two massless springs of spring constants k₁ and k₂. They have equal maximum velocity when executing simple harmonic motion. The ratio of their amplitudes is

• ${\left(\frac{{\mathrm{k}}_1}{{\mathrm{k}}_2}\right)}^{1/2}$

• $\left(\frac{{\mathrm{k}}_1}{{\mathrm{k}}_2}\right)$

• $\left(\frac{{\mathrm{k}}_2}{{\mathrm{k}}_1}\right)$

• ${\left(\frac{{\mathrm{k}}_2}{{\mathrm{k}}_1}\right)}^{1/2}$

The simple harmonic motion of a particle is given by x = a sin 2$\mathrm{\pi }$t. Then, the location of the particle from its mean position at a time 1/8th of a second is

• a

• $\frac{\mathrm{a}}{2}$

• $\frac{\mathrm{a}}{\sqrt{2}}$

• $\frac{\mathrm{a}}{4}$

The time-period of a simple pendulum of length $\sqrt{5}$ m suspended in a car moving with uniform acceleration of 5ms^-2 in a horizontal straight road is (g = 10 ms^-2)

• $\frac{2\mathrm{\pi }}{\sqrt{5}} \mathrm{s}$

• $\frac{\mathrm{\pi }}{\sqrt{5}} \mathrm{s}$

• $5\mathrm{\pi } \mathrm{s}$

• $4\mathrm{\pi } \mathrm{s}$