 Multiple Choice Questions
Multiple Choice QuestionsThe period of a simple pendulum inside a stationary lift is T. The lift accelerates upwards with an acceleration of g/3. The time period of pendulum will be
The total energy of a simple harmonic oscillator is proportional to
square root of displacement
velocity
square of the amplitude
amplitude
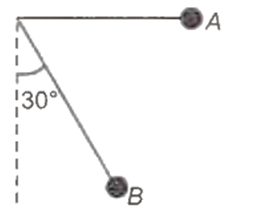
A simple pendulum is released from A as shown. If m and l represent the mass of the bob and length of the pendulum, the gain in kinetic energy at B is
C.
Loss of potential energy in coming from A to B
= mgh = mgl cos 30°
=
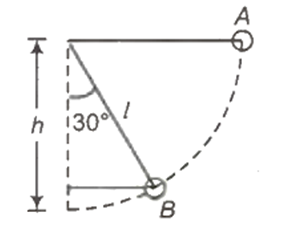
Kinetic energy gained = loss of potential energy
=
In damped oscillations, the amplitude of oscillations is reduced to one-third of its initial value a0 at the end of 100 oscillations. When the oscillator completes 200 oscillations, its amplitude must be
A particle executes simple harmonic motion with a time period of 16 s. At time t = 2 s, the particle crosses the mean position while at t = 4s, its velocity is 4 ms-1. The amplitude of motion in metre is
For a simple pendulum, the graph between T2 L and is
a straight line passing through the origin
parabola
circle
ellipse
The mstantaneous displacement of a simple harmonic oscillator is given by . Its speed will be maximum at the time
A particle of mass 5 g is executing simple harmonic motion with amplitude of 0.3 m and time period s. The maximumvalue of the force acting on the particle is
5 N
4 N
0.15 N
0.3 N
A simple pendulum has a time period T when on the earth's surface and T2 when taken to a height 2R above the earth's surface where R is the radius ofthe earth. The value of (T1 /T2) is
3
9
