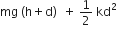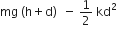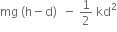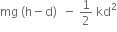Multiple Choice Questions
Multiple Choice QuestionsWhich one of the following equations of motion represents simple harmonic motion?
Acceleration = -ko x +k1x2
Acceleration =-k(x+a)
Acceleration = k (x+a)
Acceleration = k (x+a)
Each on the two strings of length 51.6 cm and 49.1 cm are tensioned separately by 20 N force. Mass per unit length of both the strings is same and equal to 1 gm-1. When both strings vibrate simultaneously the number of beats is
5
7
8
8
A block of mass M is attached to the lower end of a vertical strong. The string is hung from a ceiling and has to force constant value k. The mass is released from rest with the spring initially unstretched. The maximum extension produced in the length of the spring will be
Mg/k
2Mg//k
4 Mg/ k
4 Mg/ k
Two simple harmonic motions of angular frequency 100 and 1000 rad s-1 have the same displacement amplitude. The ratio of their maximum acceleration is
1:10
1:102
1:103
1:103
A point performs simple harmonic oscillation of period T and the equation of motion is given x = a sin (ωt + π/6). After the elapse of what fraction of the time period the velocity of the point will be equal to half of its maximum velocity?
T/8
T/6
T/3
T/3
A particle executes simple harmonic oscillation with an amplitude a. The period of oscillation is T. The minimum time taken by the particle to travel half of the amplitude from the equilibrium position is:
T/4
T/8
T/12
T/12
C.
T/12
Let displacement equation of particle executing SHM is
y = a sin ωt
As particle travels half of the amplitude from the equilibrium position, so
y= a/2
therefore,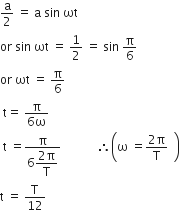
Hence, the particle travels half of the amplitude from the equilibrium in T/12 sec.
The particle executing simple harmonic motion has a kinetic energy Ko cos2 ωt. The maximum values of the potential energy and the toatal energy are respectively:
0 and 2Ko
Ko/2 and K0
Ko and 2Ko
Ko and 2Ko
A mass of 2.0 Kg is put on a flat pan attached to a vertical spring fixed on the ground as shown in the figure. The mass of the spring and the pan is negligible. When pressed slightly and released the mass executes a simple harmonic motion. The spring constant is 200 N/m. What should be the minimum amplitude of the motion, so that the mass gets detached from the pan?
Take g = `10 m/s2
8.0 cm
10.0 cm
any value less than 12.0 cm
any value less than 12.0 cm
The phase difference between the instantaneous velocity and acceleration of a particle executing simple harmonic motion is:
0.5π
π
0.707 π
0.707 π
A vertical spring with force constant k is fixed on a table. A ball of mass m at a height h above the free upper end of the spring falls vertically in the spring. so that the spring is compressed by a distance d. The net work done in the process is: