A system consists of 3 particles each of mass m located at points (1, 1), (2, 2) and (3, 3). The coordinates of the centre of mass are

• (6,6)

• (3,3)

• (1,1)

• (2,2)

A wheel of moment of inertia 2.5 kg-m² has an initial angular velocity of 40 rads^-1. A constant torque of 10 Nm acts on the wheel. The time during which the wheel is accelerated to 60 rads^-1 is 

• 4 s

• 6 s

• 5 s

• 2.5 s

A thin circular ring of mass M and radius R rotates about an axis through its centre and perpendicular to its plane, with a constant angular velocity ω. Four small spheres each of mass m (negligible radius) are kept gently to the opposite ends of two mutually perpendicular diameters of the ring. The new angular velocity of the ring will be

• 4ω

• $\frac{\mathrm{M}}{4\mathrm{m}} \mathrm{\omega }$

• $\left(\frac{\mathrm{M}}{\mathrm{M} + 4\mathrm{m}}\right) \mathrm{\omega }$

• $\left(\frac{\mathrm{M}}{\mathrm{M} - 4\mathrm{m}}\right) \mathrm{\omega }$

The angular velocity of a wheel increases from 100 rps to 300 rps in 10 s. The number of revolutions made during that time is

• 600

• 1500

• 2000

• 3000

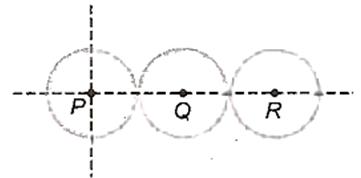
Three identical spheres, each of mass 3 kg are placed touching each other with their centres lying on a straight line. The centres of the sphere are marked at P, Q and R respectively. The distance of centre of mass of system from P is

• $\frac{\mathrm{PQ}\hspace{0.17em}+ \mathrm{QR} + \mathrm{PR}}{3}$

• $\frac{\mathrm{PQ} + \mathrm{PR}}{3}$

• $\frac{\mathrm{PQ} + \mathrm{QR} + \mathrm{PR}}{9}$

• $\frac{\mathrm{PQ} + \mathrm{PR}}{9}$

The position of a particle is given by $\mathrm{r} = \hat{\mathrm{i}} + 2\hat{\mathrm{j}} - \hat{\mathrm{k}}$ and its linear momentum is given by $\mathrm{p} = 3\hat{\mathrm{i}} + 4\hat{\mathrm{j}} - 2\hat{\mathrm{k}}$. Then its angular momentum, about the origin is perpendicular to

• yz-plane

• z-axis

• y-axis

• x-axis

A sphere of mass m and redius r rolls on a horizontal plane without slipping with the speed u. Now, if it rolls up vertically, the maximum height it would attain will be

• $\frac{3{\mathrm{u}}^2}{4\mathrm{g}}$

• $\frac{5{\mathrm{u}}^2}{2\mathrm{g}}$

• $\frac{7{\mathrm{u}}^2}{10\mathrm{g}}$

• $\frac{{\mathrm{u}}^2}{2\mathrm{g}}$

If the earth were to contract such that its radius becomes one quarter, without change in its mass, the duration of one full day would be

• 3 h

• 1.5 h

• 6 h

• 4 h

A stone of mass m tied to a string of length l is rotating along a circular path with constant speed v. The torque on the stone is

• mlv

• $\frac{\mathrm{mv}}{\mathrm{l}}$

• zero

• mv²l

The distance between the centres of carbon and oxygen atoms in the carbon monoxide molecule is 1.130 $\stackrel{\circ }{\mathrm{A}}$. Locate the centre of mass of the molecule relative to the carbon atom

• $5.428 \stackrel{\circ }{\mathrm{A}}$

• $1.130 \stackrel{\circ }{\mathrm{A}}$

• $0.6457 \stackrel{\circ }{\mathrm{A}}$

• $0.3260 \stackrel{\circ }{\mathrm{A}}$