A circular platform is mounted on the frictionless vertical axle. Its radius R =2 m and its moment of inertia about the axle is 200 kg m². It is initially at rest. A 50 kg man stands on the edge of the platform and begins to walk along the edge at the speed of 1 ms^-1 relative to the ground. Time taken by the man to complete one revolution is

• π sec

• 3π/2 sec

• 2π sec

• 2π sec

The moment of inertia of a uniform circular disc is maximum about an axis perpendicular to the disc and passing through

• B

• C

• D

• D

When a string is divided into three segments of length l₁, l₂, and l₃ the fundamental frequencies of these three segments are v₁, v₂, and v₃ respectively. The original fundamental frequency (v) of the string is

• 

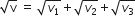
• v = v₁ +v₂ +v₃

• 
• 

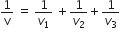
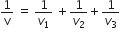
When a mass is rotating in a plane about a fixed point, its angular momentum is directed along

• a line perpendicular to the plane of rotation

• the line making an angle of 45^o to the plane of rotation

• the radius

• the radius

Two persons of masses 55 kg and 65 kg respectively. are at the opposite ends of the boat. The length of the boat is 3.0 m and weigh 100 kg. The 55 kg man walks to the 65 kg man and sits with him. If the boat is in still water the centre of mass of the system shifts by

• 3.0 m

• 2.3 m

• zero

• zero

ABC is an equilateral triangle with O as its centre F₁, F₂ and F₃ represent three forces acting on the sides AB, BC and AC respectively. If the total torque about O zero then the magnitude of F₃ is

• F₁ +F₂

• F₁ - F₂

• F₁ +F₂/2

• F₁ +F₂/2

97.

A rod PQ of mass M and length L is hinged at end P. The rod is kept horizontal by a massless string tied to point Q as shown in the figure. When a string is cut, the initial angular acceleration of the rod is,

• 3g / 2L

• g/L

• 2g/L

• 2g/L

A small object of uniform density rolls up a curved surface with an initial velocity v'. It reaches up to a maximum height of 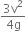 with respect to the initial position. The object is,

• ring

• solid sphere

• hollow sphere

• hollow sphere

A particle moves in a circle of radius 5 cm with constant speed and time period 0.2 πs. The acceleration of the particle is 

• 25 m/s²

• 36 m/s²

• 5 m/s²

• 5 m/s²

The instantaneous angular position of a point on a rotation wheel is given by the equation 

Q(t)  = 2t³ - 6t²

The torque on the wheel becomes zero at

• t = 0.5 s 

• t = 0.25 s

• t = 2s

• t = 2s