The chord AB of a circle of centre O subtends an angle θ with the tangent at A to the circle. Then measure of 

• θ

• 90° - θ

• 90° + θ

• 2 (180° - θ)

XYZ is a right angled triangle and ∠Y = 90°. If XY = 2.5 cm and YZ = 6 cm, then the circumradius of Δ XYZ is:

• 6.5 cm

• 3.25 cm

• 3 cm

• 2.5 cm

A 8 cm long perpendicular is drawn from the centre of a circle to a 12cm long chord. The diameter of the circle is

• 10 cm

• 12 cm

• 16 cm

• 20 cm

44.

Δ ABC a right-angled triangle has ∠B = 90° and AC is hypotenuse. D is its circumcentre and AB = 3 cm, BC = 4 cm. The value of BD is:

• 3 cm

• 4 cm

• 2.5 cm

• 5.5 cm

If a circle of radius 12 cm is divided into two equal parts by one concentric circle, then radius of inner circle is

• 6 cm

• 4 cm

• 

• 

Two circles touch externally. The sum of their areas is and the distance between their centres is 14 cm. The radius of the bigger circle is

• 22 cm

• 11 cm

• 33 cm

• 44 cm

If S is the circumcentre of Δ ABC and ∠A = 50° then the value of ∠BCS is

• 20°

• 40°

• 60°

• 80°

BC is the chord of a circle with centre O. A is a point on major arc BC as shown in the above figure. What is the value of ∠BAC + ∠OBC = ?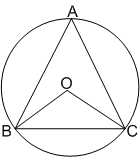

• 120°

• 60°

• 90°

• 180°

Two circles with radii 5 cm and 8 cm touch each other externally at a point A. If a straight line through the point A cuts the circles at points P and Q respectively, then AP : AQ is

• 8 : 5

• 5 : 8

• 3 : 4

• 4 : 5

AC and BC are two equal chords of a circle. BA is produced to any point P and CP, when joined cuts the circle at T. Then, 

• CT : TP  = AB : CA

• CT : TP  = CA : AB

• CT : CB  = CA : CP

• CT : CB  = CP : CA