The midpoints of AB and AC of triangle ABC are X and Y respectively. If BC + XY = 12 units, then BC - XY  is

• 10 units

• 8 units

• 6 units

• 6 units

In an isosceles  AD is the median to the unequal side meeting BC at D. DP is the angle bisector of  and PQ is drawn parallel to BC meeting AC at Q. Then the measure of  is

23.

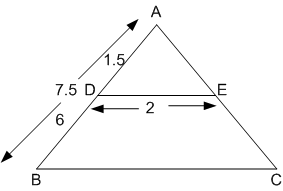
If in △ ABC, DE ∥ BC, AB = 7.5 cm, BD = 6 cm and DE = 2 cm then the length of BC in cm is

• 6

• 8

• 10

• 10

Suppose that the medians BD, CE and AF of a triangle ABC meet at G. Then AG : GF is

• 1: 2

• 2 : 1

• 1 : 3

• 1 : 3

In ΔABC, AC = BC and ∠ABC = 50°, the side BC is produced to D so that BC = CD then the value of ∠BAD is

• 80°

• 40°

• 90°

• 90°

ΔABC is isosceles having AB = AC and ∠A = 40°. Bisectors PO and OQ of the exterior angles ∠ABD and ∠ACE formed by producing BC on both sides, meet at O. Then the value of ∠BOC is

• 70°

• 110°

• 80°

• 80°

ΔABC is a triangle, PQ is line segment intersecting AB in P and AC in Q and PQ || BC. The ratio of AP : BP = 3 : 5 and length of PQ is 18 cm. The length of BC is

• 28 cm

• 48 cm

• 84 cm

• 84 cm

If the sides of a triangle are in the ratio 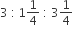 then the triangle is 

• Right triangle

• Obtuse triangle

• Equiangular triangle

• Equiangular triangle

In a right angled triangle ΔPQR, PR is the hypotenuse of length 20 cm,  the area of the triangle is

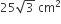
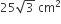
ABC is a triangle in which DE || BC and AD : DB = 5 : 4. Then DE : BC is

• 4 : 5

• 4 : 9

• 9 : 5

• 9 : 5