In Δ ABC,  and , if BD = 3 cm and CD = 4 cm, then the length of AD is

• 3.5 cm

• 5 cm

• 
• 

The centroid of a Δ ABC is G. The area of Δ ABC is 60 cm². The area of ΔGBC is

• 10 cm²

• 30 cm²

• 40 cm²

• 40 cm²

AD is perpendicular to the internal bisector of  of Δ ABC. DE is drawn through D and Parallel to BC to meet AC at E. If the length of AC is 12 cm, then the length of AE (in cm.) is

• 3

• 8

• 4

• 4

Δ ABC is similar to ΔDEF. If the area of ΔABC is 9 sq. cm. and the area of ΔDEF is 16 sq. cm. and BC = 2.1 cm, then the length of EF will be

• 5.6 cm

• 2.8 cm.

• 3.7 cm.

• 3.7 cm.

Let G be the centroid of the equilateral triangle ABC of perimeter 24 cm. Then the length of AG is

• 2√3 cm

• 8⁄√3 cm

• 8√3 cm

• 3√8 cm

If D and E are the mid-points of AB and AC respectively of ΔABC, then the ratio of the areas of Δ ADE and ◻BCED is

• 1 : 2

• 1 : 4

• 3 : 1

• 1 : 3

O is the circumcentre of the isosceles △ABC. Given that AB = AC = 5 cm and BC = 6 cm. The radius of the circle is

• 3.015 cm

• 3.205 cm

• 3.025 cm

• 3.125 cm

58.

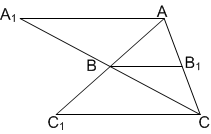
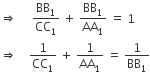
B₁ is a point on the side AC of ΔABC and B₁B is joined. A line is drawn through A parallel to B₁B meeting BC at A₁ and another line is drawn through C parallel to B₁B meeting AB produced at C₁. Then

• 

• 

• 

• 

I is the incentre of Δ ABC and if ∠BAC = 70°, then ∠BIC is

• 140°

• 55°

• 125°

• 35°

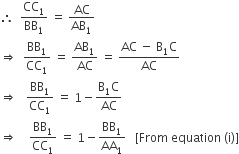
In a Δ ABC, D and E are points on AC and BC respectively, AB and DE are perpendicular to BC. If AB = 9cm, DE = 3 cm and AC  = 24 cm, then AD is

• 32 cm

• 16 cm

• 8 cm

• 4 cm