Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

81.
G is the centroid of the equilateral Δ ABC, if AB = 9 cm, then AG is equal to:

$3 square root of 3 space cm$

3 cm

^{$fraction numerator 3 square root of 3 over denominator 2 end fraction cm$}

6 cm

$3 square root of 3 space cm$

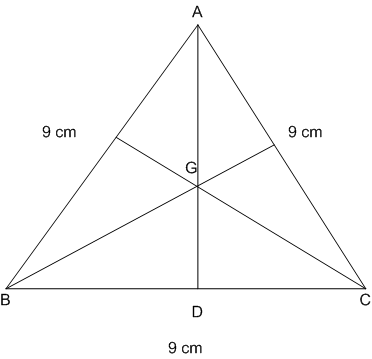
Median AD of equilateral triangle:
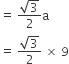
$equals space fraction numerator square root of 3 over denominator 2 end fraction straight a equals space fraction numerator square root of 3 over denominator 2 end fraction space cross times space 9$
As Centroid divides the median in the ratio of 2 : 1.
∴ AG : GD = 2 : 1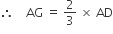
$therefore space space space space AG space equals space 2 over 3 space cross times space AD$
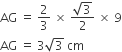
$AG space equals space 2 over 3 space cross times space fraction numerator square root of 3 over denominator 2 end fraction space cross times space 9 AG space equals space 3 square root of 3 space cm$

129 Views

82.

In the figure (not drawn to scale) given below, if AD = DC = BC and $angle BCE space equals space 96 degree$ , then $angle BCE space space equals space 96 degree comma$ then $angle DBC$ is

32°
84°
64°
96°

92 Views

83.

In Δ ABC, $angle straight B space equals space 5 angle straight C$ and $angle straight A space equals space 3 angle straight C$ , then the measure of $angle straight C$ is