Multiple Choice QuestionsA telegraph post is bent at a point above the ground due to storm. Its top just touches the ground at a distance of 10√3 from its foot and makes an angle of 30° with the horizontal. Then height (in metres) of the telegraph post is
30
24
20
28
A vertical tower stands on a horizontal plane and is surmounted by a vertical flag staff of height h. At a point on the plane, the angle of elevation of the bottom of the flag staff is α and that of the top of the flag staff is β. Then the height of the tower is
A man on the top of a tower, standing on the sea shore, finds that a boat coming towards him takes 10 minutes for the angle of depression to change from 30° to 60°. How soon the boat reach the sea-shore?
5 minutes
7 minutes
10 minutes
50 minutes
From the top of a cliff 100 metre high, the angles of depression of the top and bottom of a tower are 45° and 60° respectively. The height of the tower is
A person from the top of a hill observes a vehicle moving towards him at a uniform speed. It takes 10 minutes for the angle of depression to change from 45° to 60°. After this the time required by the vehicle to reach the bottom of the hill is
12 minutes 20 seconds
13 minutes
13 minutes 40 seconds
14 minutes 24 seconds
C.
13 minutes 40 seconds
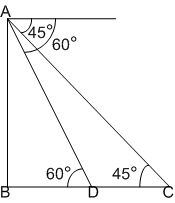
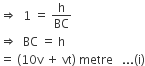
A man standing on the bank of a river observes that the angle of elevation of the top of a tree just on the opposite bank is 60°. But the angle of elevation is 30° from a point which is at a distance of 
 from the bank. Then the height of the tree
60 ft
45 ft
30 ft
30 ft
The shadow of a vertical tower on ground level increases by 10 m when the altitude of the sun changes from 45° to 30°. The height of the tower is
5( √3 + 1 ) m
10( √3 - 1 ) m
9 m
13 m
Two men are on opposite sides of a tower. They measure the angles of elevation of the top of the tower as 30° and 45° respectively. If the height of the tower is 50 m, the distance between the two men isÂ
136.5 m
50√3 m
100√3 m
135.5 m
The shadow of a tower when the angle of elevation of the sun is 45°, is found to be 10 m longer than when it was 60°. The height of the tower is
5( √3 - 1 ) m
5( √3 + 3 ) m
10( √3 - 1 ) m
10( √3 + 1 ) m
The angle of elevation of aeroplane from a point on the ground is 45°. After flying 15 sec, the elevation changes to 30°. If the aeroplane is flying at a height of 2500 m, then the speed of the aeroplane in km/hr is
600
600( √3 + 1 )
600√3
600( √3 - 1 )
Switch
