31.

An employer reduces the number of his employees in the ratio 9 : 8 and increases their wages in the ratio 14 : 15. If the original wage bill was ₹ 18,900, find the ratio in which the wage bill is decreased.

• 20 : 21

• 21 : 20

• 20 : 19

• 20 : 19

There is a ratio of 5 : 4 between two numbers. If 40 percent of the first is 12, then 50% of the second number is

• 12

• 24

• 18

• 18

The students in three classes are in the ratio 4 : 6 : 9. If 12 students are increased in each class, the ratio changes to 7 : 9 : 12. Then the total number of students in the three classes before the increase is

• 95

• 76

• 100

• 100

₹ 864 is divided among A, B and C such that 8 times A's share is equal to 12 times B's share and also equal to 6 times C's share. How much did B get?

• ₹ 399

• ₹ 192

• ₹ 288

• ₹ 288

The population of a town is 3,11,250. The ratio between women and men is 43 : 40. If there are 24% literate among men and 8% literate among women, the total number of literate persons in the town is

• 41,800

• 48,900

• 56,800

• 56,800

Annual income of Amit and Veeri are in the ratio 3 : 2, while the ratio of their expenses is 5 : 3. If at the end of year each saves ₹ 1,000, the annual income of Amit is

• ₹ 9,000

• ₹ 8,000

• ₹ 7,000

• ₹ 7,000

If A : B = 2 : 3,  B : C = 4 : 5  and C : D = 5 : 9, then A : D is equal to

• 11 : 17

• 8 : 27

• 5 : 9

• 5 : 9

Rs. 1050 are divided among A, B and C in such a way that the share of A is 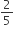 of the combined share of B and C. A will get

• Rs. 200

• Rs. 300

• Rs. 320

• Rs. 320

If A : B = 2 : 3  and B : C = 3 : 7, then A + B : B + C : C + A is

• 4 : 8 : 9

• 5 : 8 : 9

• 5 : 10 : 9

• 5 : 10 : 9

If  and , then the ratio 2x : 3y equals

• 4 : 1

• 2 : 3

• 4 : 3
• 4 : 3