X and Y are centres of circles of radii 9cm and 2 cm respectively, XY = 17cm. Z is the centre of a circle of radius r cm which touches the above circles externally. Given that  the value of r is

• 13 cm

• 6 cm

• 9 cm

• 9 cm

AB and CD are two parallel chords of a circle of lengths 10 cm and 4 cm respectively. If the chords are on the same side of the centre and the distance between them is 3 cm, then the diameter of the circle is

A chord of a circle is equal to its radius. The angle subtended by this chord at a point on the circumference is

• 80°

• 60°

• 30°

• 90°

ABC is a isosceles triangle inscribed in a circle. If AB = AC = 12√5 cm and BC = 24 cm then the radius of circle is

• 10 cm

• 15 cm

• 12 cm

• 14 cm

ABC is an isosceles triangle where AB = AC which is circumscribed about a circle. If P is the point where the circle touches the side BC, then which of the following is true?

• BP = PC

• BP > PC

• BP < PC

• BP ≥ PC

Let two chords AB and AC of the larger circle touch the smaller circle having same centre at X and Y. Then XY = ?

• BC

• 1/2 BC

• 1/3 BC

• 2/3 BC

A chord of length 39 cm is at a distance of 10.4 cm from the centre of a circle. Find the radius of the circle.

• 19.5 cm (appr)

• 22.1 cm (appr)

• 28.6 cm (appr)

• 28.6 cm (appr)

A chord of length 10 cm subtends an angle 120° at the centre of the circle. Distance of the chord from the centre is

•  

  

•  

  

•  

  

•  

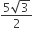
  5

Length of a chord PQ of a circle with centre O is 4 cm. If the distance of PQ from the point O is 2 cm, then the length of the diameter is

• 2√2

• 3√2

• 5√2

• 4√2

30.

P, Q R are the points so that PR = 3 cm, QR = 5 cm and PQ = 8 cm. The number of circle passing through the points P, Q, R is

• 3

• 2

• 1

• 1