 Multiple Choice Questions
Multiple Choice QuestionsThe radius of a circle is 13 cm and xy is a chord which is at a distance of 12 cm from the centre. The length of the chord is
12 cm
10 cm
20 cm
15 cm
Two equal circles pass through each other's centre. If the radius of each circle is 5 cm, what is the length of the common chord?
5√3
10√3
5√3 / 2
5
P and Q are the midpoints of two chords (not diameter) AB and AC of a circle with center O. OP and OQ lines are extended to points S and R respectively, to touch the circle. In major arc T is another point between R and S. Then if ∠BAC = 32° then ∠RTS = ?
74°
106°
64°
32°
A.
74°
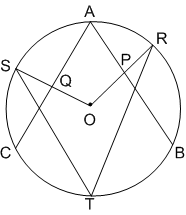
P and Q are mid points of AC and AB chords of a circle
![]()
Now, in a quadrilateral, APOQ
![]()
[AS, Angle subtended by an arc at the centre is double the angle subtended by an arc at any point in remaining part of the circle].
If O be the circumcentre of a Δ PQR and ∠QOR = 110°, ∠OPR = 25° then the measure of ∠PRQ is
50°
55°
60°
65°
A, B, C, D are four points on a circle. AC and BD intersect at a point E such that ∠BEC = 130° and ∠ECD = 20°. Then, ∠BAC is
90°
100°
110°
120°
N is the foot of the perpendicular from a point P of a circle with radius 7 cm, on a diameter AB of the circle. If the length of the chord PB is 12 cm, the distance of the point N from the point B is
![]()
![]()
![]()
![]()
Two circles of same radius 5 cm, intersect each other at A and B. If AB = 8 cm, then the distance between the centres is
10 cm
4 cm
6 cm
8 cm
Each of the two circles same radius a passes through the centre of the other. If the circles cut each other at the points A, B and O, O' be their centres, area of the quadrilateral AOBO' is
![]()
![]()
![]()
a2
In a circle of radius 17 cm, two parallel chords of lengths 30 cm and 16 cm are drawn. If both the chords are on the same side of the centre, then the distance between the chords is
9 cm
7 cm
23 cm
11 cm
Two circles touch each other internally, Their radii are 2 cm and 3 cm. The biggest chord of the greater circle which is outside the inner circle is of length
2√2 cm
3√2 cm
2√3 cm
4√2 cm
