 Multiple Choice Questions
Multiple Choice QuestionsThe ratio between the height of tower and the point at some distance is  . What will be the angle of elevation?
. What will be the angle of elevation?




Two towers A and B have lengths 45m and 15 m respectively. The angle of elevation from the bottom of the B tower to the top of the A tower is  . If the angle of elevation from the bottom of the A tower to the top of the B tower is
. If the angle of elevation from the bottom of the A tower to the top of the B tower is  , then the value of
, then the value of  is
is




The shadow of a tower standing on a level ground is found to be 40 m longer when the sun's altitude is  , then when it is
, then when it is  . Find the length of the tower.
. Find the length of the tower.
10 m

20 m
20 m
D.
20 m
Let AB = h m be the height of a tower.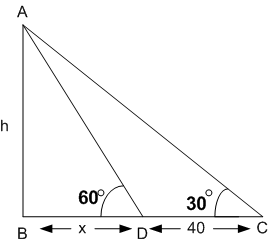
In 


 ...(i)
...(i)
Now in  ,
,




[From Eq. (i)]





Hence, the height of a tower is 
The length of a shadow of a tower is 9 m when the sun's altitude is  . What is the height of the tower?
. What is the height of the tower?




From a point, 40 m apart from the foot of a tower, the angle of elevation of its top is 60°. The height of the tower is:
40√2 cm
40√3 cm
40√3 m
40√2 m
The angles of elevation of top and bottom of a flag kept on a flag post from 30 m distance are  and
and  respectively. Height of the flag is [taking
respectively. Height of the flag is [taking  ]
]

15 m
14.32 m
14.32 m
A 25m long ladder is rested on a wall. The foot of the ladder is 7m away from the wall. If the end of the ladder (resting on the wall) slides down 4m, then how far will its foot move away?
5 m
8 m
9 m
9 m
A man standing on the bank of river observes that the angle subtended by a tree on the opposite bank is 60°. When he retires 36 m from the bank, he finds that the angle is 30°. The breadth of the river is
15 m
18 m
16 m
16 m
129 m from the foot of a cliff on level of ground, the angle of elevation of the top of a cliff is 30°. The height of this cliff is
50√3 m
45√3 m
43√3 m
44√3 m
Two ships are sailing in the sea on the two sides of a light house. The angle of elevation of the top of the light house as observed from the two ships are 30° and 45° respectively. If the light house is 100m high, the distance between the two ships is :(take √3=1.73)
173 m
200 m
273 m
373 m
