 Multiple Choice Questions
Multiple Choice QuestionsAn aeroplane flying horizontally at a height of 3 Km, above the ground is observed at a certain point on earth to subtend an angle of 60°. After 15 sec flight, its angle of elevation is changed to 30°. The speed of the aeroplane (taking √3 = 1.732) is
230.63 m/sec
230.93 m/sec
235.85 m/sec
235.85 m/sec
B.
230.93 m/sec
AB = CD = 3000 metre
A and C = Positions of aeroplane
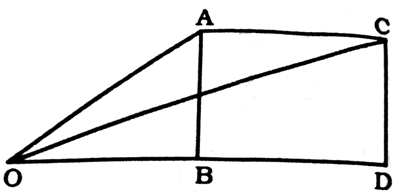
In ΔOAB,
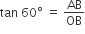
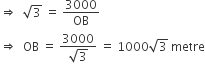
In ΔOCD,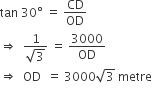

∴ Speed of aeroplane
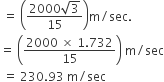
If the angle of elevation of the sun decreases from 45° to 30°, then the length of the shadow of a pillar increases by 60m. The height of the pillar is




The angle of elevation of the top of a tower, vertically erected in the middle of a paddy field, from two points on a horizontal line through the foot of the tower are given to be α and β (α>β). The height of the tower is h unit. A possible distance (in the same unit) between the points is




The angle of elevation of the top of an unfinished pillar at a point 150 metres from its base is 30°. The height (in metres) that the pillar must be raised so that its angle of elevation at the same point may be 45°, is (takeing √3 = 1.732)
63.4
86.6
126.8
128.6
From the top of a tower of height 180 m the angles of depression of two objects on either sides of the tower are 30° and 45°. Then the distance between the objects are




A tower standing on a horizontal plane subtends a certain angle at a point 160 m apart from the foot of the tower. On advancing 100 m towards it, the tower is found to subtend an angle twice as before. The height of the tower is
80 m
100 m
160 m
160 m
The angle of elevation of a tower from a distance 50 m from its foot is 30°. The height of the tower is
![]()
![]()
![]()
![]()
The length of a shadow of a vertical tower is  times its height. The angle of elevation of the Sun is
times its height. The angle of elevation of the Sun is
30°
45°
60°
60°
Two posts are x metres apart and the height of one is double that of the other. If from the mid-point of the line joining their feet, an observer finds the angular elevations of their tops to be complementary, then the height (in metres) of the shorter post is




An aeroplane when flying at a height of 5000m from the ground passes vertically above another aeroplane at an instant, when the angles of elevation of the two aeroplanes from the same point on the ground are 60° and 45° respectively. The vertical distance between the aeroplanes at that instant is




