The ratio between the length and the breadth of a rectangular park is 3 : 2. If a man cycling along the boundary of the park at the speed of 12 km/hr completes one round in 8 minutes, then the area of the park is

• 153650 sq. metre

• 135600 sq. metre

• 153600 sq. metre

• 153600 sq. metre

A rectangular park 60 metre long and 40 metre wide has two concrete crossroads running in the middle of the park and rest of the park has been used as a lawn. If the area of the lawn is 2109 m² then the width of the road is

• 3 metre

• 5 metre

• 6 metre

• 6 metre

A rectangular water tank is 80 metre x 40 metre. Water flows into it through a pipe of 40 sq. cm at the opening at a speed of 10 km/hr. The water level will rise in the tank in half an hour by

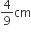
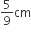
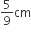
Four circles of equal radii are described about the four corners of a square so that each touches two of the other circles. If each side of the square is 140 cm and then area of the space enclosed between the circumference of the circle is 

• 4200 cm²

• 2100 cm²

• 7000 cm²

• 7200 cm²

A square and a regular hexagon are drawn such that all the vertices of the square and the hexagon are on a circle of radius r cm. The ratio of area of the square and the hexagon is

• 3 : 4

• 
• 
• 

76.

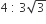
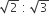
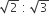
If the length and breadth of a rectangle are increased by 10% and 8% respectively, then the area of the rectangle increases by

• 
• 

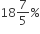
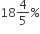
• 18%

• 18%

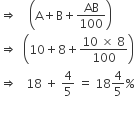
An arc AB of a circle subtends an angle x radius at the centre of the circle. Given that the area of the sector AOB is equal to the square of the length of the arc AB, then the value of x is

• 1/√2

• 1/2

• 1/√3

• 1/3

The area of the circle with radius Y is W. The difference between the areas of the bigger circle (with radius Y) and that of the smaller circle (with radius X) is W'. So X/Y is equal to:

An arc of 30° in one circle is double an arc in a second circle, the radius of which is three times the radius of the first. Then the angle subtended by the arc of the second circle at its centre is

• 3°

• 4°

• 5°

• 6°

Area of the circle inscribed in a square of diagonal  (in cm²) is