 Multiple Choice Questions
Multiple Choice QuestionsThe height of a right prism with a square base is 15 cm. If the area of the total surfaces of the prism is 608 sq. cm. its volume is
910 cm3
920 cm3
960 cm3
960 cm3
C.
960 cm3
Total surface area of prism = Curved surface area + 2 x Area of base
Curved surface area = Base Perimeter x Height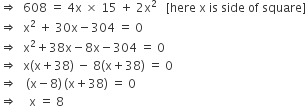
Volume of prism = Base Area x Height
= 8 x 8 x 15 = 960 cm3
The height of a circular cylinder is increased six times and the base area is decreased to one-ninth of its value. The factor by which the lateral surface of the cylinder increases is
2
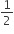


If a solid cone of volume  is kept inside a hollow cylinder whose radius and height are that of the cone, then the volume of water needed to fill the empty space is
is kept inside a hollow cylinder whose radius and height are that of the cone, then the volume of water needed to fill the empty space is




Two cm of rain has fallen on a square km of land. Assuming that 50% of the raindrops could have been collected and contained in a pool having a 100 m x 10 m base, by what level would the water level in the pool have increased?
1 km
10 m
10 cm
10 cm
A cylindrical can whose base is horizontal and is of internal radius 3.5 cm contains sufficient water so that when a solid sphere is placed inside, water just covers the sphere. The sphere fits in the can exactly. The depth of water in the can before the sphere was put is
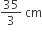
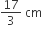
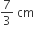
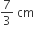
If the radius of a sphere is increased by 2m, its surface area is increased by 704 m2. What is the radius of the original sphere?
16 m
15 m
14 m
14 m
A right circular cylinder is circumscribing a hemisphere such that their bases are common. The ratio of their volumes is
1 : 3
1 : 2
2 : 3
2 : 3
The number of coins, each of radius 0.75 cm and thickness 0.2 cm, to be melted to make a right circular cylinder of height 8 cm and radius 3 cm is
640
600
500
500
Three spherical balls of radii 1 cm, 2 cm and 3 cm are melted to form a single spherical ball. In the process, the loss of material is 25%. The radius of the new ball is
6 cm
5 cm
3 cm
3 cm
