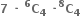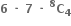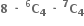Book Store

Download books and chapters from book store.
Currently only available for.
CBSE

Gujarati JEE Mathematics : ક્રમચય અને સંચય

Multiple Choice Questions

91.

એક ચૂંટણીમાં મતદાન વધુમાં વધુ જેટલા ઉમેદવાર ચૂંટવાના છે તેટલા મત આપી શકે છે. ચૂંટણીમાં 10 ઉમેદવારમાંથી 4 ઉમેદવાર ચૂંટવાના છે. જો મતદારને ઓછામાં ઓછો એક મત આપવાનો હોય, તો તે મતદાન કેટલી રીતે કરી શકે ?

385
5040
1110
6210

92. MISSISSIPPI શબ્દના અક્ષરોની ફેરબદલી કરીને કેટલા શબ્દો બનાવી શકાય કે જેથી S બે પાસપાસે ન આવે ?

$bold 7 bold space bold times bold space bold C presuperscript bold 6 subscript bold 4 bold space bold times bold C presuperscript bold 8 subscript bold 4$
$bold 6 bold space bold times bold space bold 8 bold space bold times bold space bold C presuperscript bold 7 subscript bold 4$
$bold 6 bold space bold times bold space bold 7 bold space bold times bold space bold C presuperscript bold 8 subscript bold 4$
$bold 8 bold space bold times bold space bold C presuperscript 6 subscript bold 4 bold space bold times bold space bold C presuperscript bold 7 subscript bold 4$

93. ગણ S = {1, 2, 3, ... 12} ને સમાન સભ્યોની સંખ્યાવાળા ઉપગણ A, B, C માં વિભાજન કરવામાં આવે કે જેથી A ∪ B ∪ C = S, A ∩ B = B ∩ C = A ∩ C = $up diagonal strike bold 0$ તો આ કેટલા પ્રકારે શક્ય છે ?

$fraction numerator bold 12 bold space bold factorial over denominator bold left parenthesis bold 4 bold factorial bold right parenthesis to the power of bold 4 end fraction$
$fraction numerator bold 12 bold space bold factorial over denominator bold left parenthesis bold 4 bold factorial bold right parenthesis cubed end fraction$
$fraction numerator bold 12 bold space bold factorial over denominator bold 3 bold space bold left parenthesis bold 4 bold factorial bold right parenthesis to the power of bold 4 end fraction$
$fraction numerator bold 12 bold space bold factorial over denominator bold 3 bold space bold left parenthesis bold 4 bold factorial bold right parenthesis cubed end fraction$

94. 8 સમાન દડાને ત્રણ ભિન્ન ખોખામાં કેટલી રીતે મૂકી શકાય કે જેથી એક પણ ખોખું ખાલી ન રહે ?

₈C₃
3⁸
5
21

95.

એક વિદ્યાર્થી પ્રથમ પાંચ પ્રશ્નોમાંથી ઓછામાં ઓછા ચાર પ્રશ્નોના જવાબ આપવાના હોય તે રીતે 13 પ્રશ્નોમાંથી 10 પ્રશ્નોના જવાબ કેટલી રીતે આપી શકે ?

280
346
196
140

96.

જો p અને q નો લ.સા.અ. r² t⁴ s² હોય, જ્યાં r, s, t અવિભાજ્ય પૂર્ણાંક સંખ્યાઓ છે. p અને q ધન પૂર્ણાંક છે, તો આવી ક્રમયુક્ત જોડ (p, q) ની સંખ્યા ........ છે.

252
254
224
225

97. સમતલમાં આવેલાં 10 બિંદુઓ પૈકી 6 બિંદુઓ સમરેખ છે. જો આ બધાં બિંદુઓની મદદથી ત્રિકોણ બને, તો .......

N > 190
N ≤ 100
100 < N ≤ 140
140 < N ≤ 190

98.

6 ભિન્ન નવલકથાઓ અને 3 ભિન્ન શબ્દકોશોમાંથી 4 નવલકથાઓ અને 1 શબ્દકોશ પસંદ કરીને છાજલી પર ગોઠવવામાં આવે છે. શબ્દકોશ હંમેશાં મધ્યમાં જ રહે તેવી ગોઠવણીના પ્રકારની સંખ્યા ........ છે.

ઓછામાં ઓછા 1000
500 થી ઓછા
ઓછામાં ઓછા 500 અને 750 થી ઓછા
ઓછામાં ઓછા 750 પરંતુ 1000 થી ઓછા

99.

દડાઓના રંગ સિવાય દડાઓ સમાન છે. તેમ ધારી, 10 સફેદ, 9 લીલા અને 7 કાળા રંગના દડામાંથી એક કે વધુ દડા કરેલી રીતે પસંદ કરી શકાય ?

880
879
630
629

100. વિધેય f(x) = _(7-x)P_(x-3) નો વિસ્તાર ...... છે.

{1, 2, 3, 4, 5}
{1, 2, 3, 4, 5, 6}
{1, 2, 3}
{1, 2, 3, 4}

{1, 2, 3}

Tips: -

અહીં x - 3 ≥ 0 અને 7 - x ≥ x - 3

∴ x ≥ 3 અને 10 ≥ 2x

∴ 3 ≤ x અને x ≤ 5

∴ 3 ≤ x ≤ 5

∴ x = 3, 4, અથવા 5

∴ f(3) = ₄P₀ = 1 તથા f(4) = ₃P₁ = 3 તથા f(5) = ₂P₂ = 2 ! = 2

∴ f નો વિસ્તાર = {1 , 2 , 3}

Switch

Book Store

Subject

Gujarati JEE Mathematics : ક્રમચય અને સંચય

Multiple Choice Questions

Switch