CBSE
 Multiple Choice Questions
Multiple Choice Questions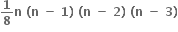
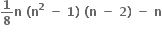
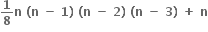
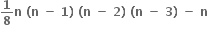
B.
219Tips: -
અહીં n (A) = 4 અને n (B) = 2 આપેલ છે. આથી n (A × B) = 4 × 2 = 8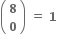
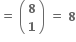
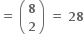
 નું અવિભાજ્ય અવયવીકરણ 2a3b5c7d ... હોય, તો નીચેનામાંથી ...... સત્ય બને છે. (જ્યાં, a, b, c, d ... ∈ N)
નું અવિભાજ્ય અવયવીકરણ 2a3b5c7d ... હોય, તો નીચેનામાંથી ...... સત્ય બને છે. (જ્યાં, a, b, c, d ... ∈ N)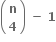
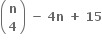
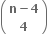
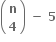
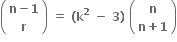 તો k ∈ .......
તો k ∈ .......



