CBSE
 Multiple Choice Questions
Multiple Choice QuestionsN-{9}
N
N ∪ {0}
{1, 3, 4, 5, 7, 9, 14}

(i)-(c), (ii)-(d), (iii)-(b), (iv)-(a)
(i)-(b), (ii)-(c), (iii)-(d), (iv)-(a)
(i)-(a), (ii)-(c), (iii)-(b), (9iv)-(d)
(i)-(a), (ii)-(b), (iii)-(c), (iv)-(d)
A.
(i)-(c), (ii)-(d), (iii)-(b), (iv)-(a)
Tips: -
ધારો કે,
A = ગણિત પસંદ હોય તેવા વિદ્યાર્થીઓનો ગણ
B = ભૌતિકવિજ્ઞાન પસંદ હોય તેવા વિદ્યાર્થીઓનો ગણ
C = રસાયણ વિજ્ઞાન પસંદ હોય તેવા વિદ્યાર્થીઓનો ગણ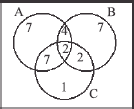
અહીં,m(A) = 20, n(B) = 15; n(C) = 12
n(C∩A) = 9, n (A ∩ B) = 6; n (B ∩ C) = 4, n (A ∩ B ∩ C) = 2 આપેલ છે. તો ઉપર આપેલી વેન આકૃતિ પરથી સ્પષ્ટ છે કે, જેમને ઓછામાં ઓછો એક વિષય પસંદ હોય તેવા વિદ્યાર્થીઊની સંખ્યા 30 છે. આમ, (i) -(c) (જવાબ નકી થયો.)
ઓછામાં ઓછા બે વિષય પસંદ હોય તેવા વિદ્યાર્થીઓની સંખ્યા 15 છે. (ii) - (d)
વધુમાં વધુ 2 વિષય પસંદ હોય તેવા વિદ્યાર્થીઓની સંખ્યા 28 છે. (iii) -- (b)
તથા એક પણ વિષય પસંદ ન હોય તેવો કોઈ વિદ્યાર્થી નથી. (iv) - (a)
આમ, (i)- (c), (ii) -(d), (iii)-(b), (iv)-(a) મળે.
10
7
9
6
A = B
B = C
A = C
આપેલ પૈકી એક પણ નહી
3
4
1
2
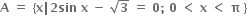 તથા
તથા 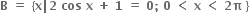 હોય, તો A ∩ B શોધો.
હોય, તો A ∩ B શોધો.



(i) -(a), (ii) - (b), (iii) - (c), (iv) - (d)
(i) - (d), (ii) - (a), (iii) - (b), (iv) - (c)
(i) - (c), (ii) - (b), (iii) - (a), (iv) - (d)
આપેલ પૈકી એક પણ નહી
135
45
90
180
1000
800
1100
1200
3200
3300
3100
3000