CBSE
 Multiple Choice Questions
Multiple Choice Questions હોય, તો f-1(x) = ......... (સ્વીકારી લો કે f-1 નું અસ્તિત્વ છે.)
હોય, તો f-1(x) = ......... (સ્વીકારી લો કે f-1 નું અસ્તિત્વ છે.)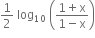


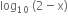
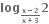 તથા g : B → R, g(x) =
તથા g : B → R, g(x) = 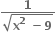 હોય, તો x ની કઈ કિંમતો માટે વિધેય
હોય, તો x ની કઈ કિંમતો માટે વિધેય  અસ્તિત્વ ધરાવે ?
અસ્તિત્વ ધરાવે ?(-3, 2)
(-∞, -3) ∪ (3, ∞)
[2,3]
[-3, -2]
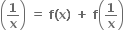 શરત સંતોષે છે. જો f(12) = 1729 હોય, તો f(15) = ............ .x ∈ R
શરત સંતોષે છે. જો f(12) = 1729 હોય, તો f(15) = ............ .x ∈ R3357
3376
2075
1001
(8, 10)
(0, 10)
(10, 12)
(4, 5)
(0, ∞)
(-∞, 0)
(-∞, ∞)
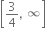
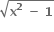 હોય, તો (gof) (x) = ......
હોય, તો (gof) (x) = ......
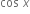
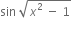
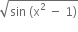
અવ્યાખ્યાયિત
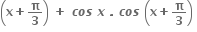 તથા g
તથા g  = 1 હોય તો (gof) (x) = ............ .
= 1 હોય તો (gof) (x) = ............ .
1
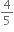
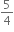
અવ્યાખ્યાયિત
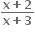 નું પ્રતિવિધેય અસ્તિત્વ ધરાવતો x ∈ ........... માટે, f-1(x) > 0 મળે.
નું પ્રતિવિધેય અસ્તિત્વ ધરાવતો x ∈ ........... માટે, f-1(x) > 0 મળે.
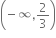
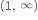
શક્ય નથી.
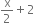
y = ±
y = ±x + 4
y = x ± 2
y = ± x ± 2
{0, 1, -1}
{0, -1}

B.
{0, -1}
Tips: -
x1, x2 ∈ R માટે, જો f(x1) = f(x2) લઈએ, તો
(x1 + 1)2 = (x2 + 1)2-1 (જ્યાં x1, x2 ≥ -1 )
∴ (x1 + 1)2 = (x2 + 1)2
∴ x1 + 1 = x2 + 1 અથવા x1 + 1 = -x2 - 1
∴ x1 = x2 અથવા x1 + x2 = -2 પરંતુ x1x2 ≥ - 1 હોવાથી x1 + x2 = -2 થવા માટે, x1 = x2 = -1 મળે.
આમ, f(x1) = f(x2) ⇒ x1 = x2 હોવાથી, f એક-એક વિધેય છે.
હવે, 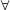 y, y ≥ -1, f(x) = (x+1)2 - 1 = y લેતાં,
y, y ≥ -1, f(x) = (x+1)2 - 1 = y લેતાં,
(x+1)2 = y + 1
∴ x + 1 = 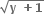 (x ≥-1)
(x ≥-1)
∴ x = -1 + 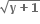 મળે. ... (1)
મળે. ... (1)
∴ f(x) = f(-1 + 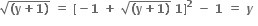
આમ, f વ્યાપ્ત વિધેય હોવાથી, f-1(x) અસ્તિત્વ ધરાવે.
હવે, f(x) = f-1(x) હોવાથી,
(x+1)2 -1 = -1 + 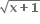 (f(x) = y ⇒ x = f-1(y))
(f(x) = y ⇒ x = f-1(y))
∴ (x+1)2 = 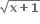
∴ (x+1)2 = 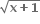 = 0
= 0
∴ 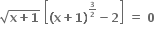
∴ 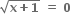 અથવા
અથવા 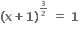
∴ x + 1 = 0 અથવા (x + 1)3 = 1 ⇒ x = 0
આમ x = 0 , અથવા - 1 મળે.
S { x | f(x) = f-1(x)} હોય, તો S = {0, -1} મળે.