CBSE
 Multiple Choice Questions
Multiple Choice Questions એ એક-એક તથા વ્યાપ્ત વિધેય હોય તો B =
એ એક-એક તથા વ્યાપ્ત વિધેય હોય તો B =




B.

Tips: -
f(x) = tan-1  આપેલ છે.
આપેલ છે.
x = tan θ જ્યાં, θ ∈ 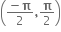 ⇒ θ = tan-1 x
⇒ θ = tan-1 x
પરંતું x ∈ (-1, 1) હોવાથી, θ ∈ 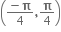 મળે.
મળે.
હવે f(x) = tan-1 
= tan-1 (tan 2θ)
વળી, 
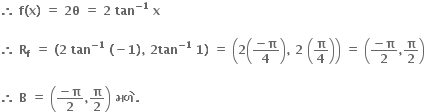
 cos + 1 વ્યાપ્ત વિધેય હોય, તો S = .......... .
cos + 1 વ્યાપ્ત વિધેય હોય, તો S = .......... .
[0, 3]
[-1, 3]
[-1, 1]
[0, 1]
f-1(f(A))=A
f-1(f(A)) ⊄ A
f(f-1(N))=B
અપેલ પૈકી એક પણ નહી
 ] x ; જ્યાં [x] એ પૂર્ણાંક ભાગ વિધેય દર્શાવે છે, તો નીચેનામાંથી કયું સત્ય છે ?
] x ; જ્યાં [x] એ પૂર્ણાંક ભાગ વિધેય દર્શાવે છે, તો નીચેનામાંથી કયું સત્ય છે ?




 ))}}] = .......
))}}] = .......
12
8
4
16
36, 0, 0
0, 0, 36
0, 36, 0
36, 6, 0

 x ∈ R તથા g(x) =
x ∈ R તથા g(x) = 
 x ∈ R, (fog) (x) તથા (gof) (x) ને f(g(x)) તથા g(f(x)) થી દર્શાવીએ તો નીચેનામાંથી શું સત્ય બને ?
x ∈ R, (fog) (x) તથા (gof) (x) ને f(g(x)) તથા g(f(x)) થી દર્શાવીએ તો નીચેનામાંથી શું સત્ય બને ? f નો વિસ્તાર  છે
છે
fog નો વિસ્તાર  છે.
છે.

કોઈ એવો મળે કે જેથી




S1 = {(x,a)|a=x+2, x ∈ X, a ∈ Y} સંબંધ દર્શાવે પરંતુ X થી Y પરનું વિધેય નથી.



