CBSE
 Multiple Choice Questions
Multiple Choice Questionsn = 4 માટે સત્ય નથી.
 n ∈ N
n ∈ N
r !
n!
n+r+1
(n+r)!
1275
1225
2450
1375
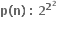 નો એકમનો અંક ....... છે. n > 1
નો એકમનો અંક ....... છે. n > 1
0
4
6
2
 n ∈ N
n ∈ N
 n ∈ N, n > 1
n ∈ N, n > 1
 n ∈ N, n ≥ 3
n ∈ N, n ≥ 3
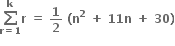 તો k =- ....... .
તો k =- ....... .
n + 6
n + 7
n + 5
n + 4
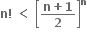 નું પાલન થાય તેવો નાનામાં નાનો ધનપૂર્ણાંક ........ છે. જ્યાં [] મહત્તમ પૂર્ણાંક વિધેય છે.
નું પાલન થાય તેવો નાનામાં નાનો ધનપૂર્ણાંક ........ છે. જ્યાં [] મહત્તમ પૂર્ણાંક વિધેય છે.
6
3
4
2
1
4
2
5
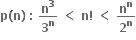 દરેક n ≥ k, n ∈ N માટે સત્ય છે, તો k = .......... .
દરેક n ≥ k, n ∈ N માટે સત્ય છે, તો k = .......... .
6
5
4
3
A.
6
Tips: -
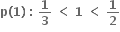 સત્ય નથી.
સત્ય નથી.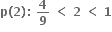 સત્ય નથી.
સત્ય નથી.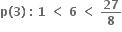 સત્ય નથી.
સત્ય નથી. 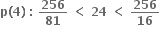 સત્ય નથી.
સત્ય નથી. 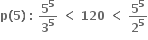 એટલે કે
એટલે કે 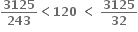 સત્ય નથી.
સત્ય નથી.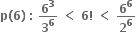 એટલે કે
એટલે કે 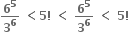 એટલે કે
એટલે કે 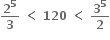
એટલે કે 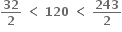 સત્ય છે.
સત્ય છે.
આ જ રીતે, સાબિત કરી શકાય કે p(n) દરેક n > 6 માટે સત્ય છે.
અહીં ગણિતીય અનુમાનના સિદ્વાંત પરથી 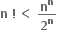 અને
અને 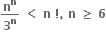 સાબિત કરી શકાય.
સાબિત કરી શકાય.
 n ∈ N .......... ના ગુણકમાં છે.
n ∈ N .......... ના ગુણકમાં છે.
4
7
5
2