CBSE
 Multiple Choice Questions
Multiple Choice Questions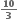 = log2y + logy2 તથા x ≠ y હોય તો x+y = ......
= log2y + logy2 તથા x ≠ y હોય તો x+y = ......

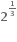
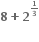
C.
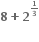
Tips: -
અહીં log2 x + logx 2 =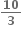 = log2 y + logy 2 આપેલ છે.
= log2 y + logy 2 આપેલ છે.  લેતાં, =
લેતાં, = 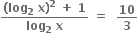
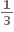
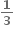
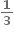 મળે.
મળે.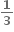 થાય.
થાય. 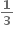 લેતાં, log2 y = 3 થાય.
લેતાં, log2 y = 3 થાય. 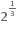 અથવા x =
અથવા x = 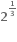 અને y = 23થાય
અને y = 23થાય
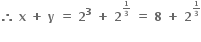
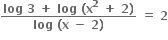 ના ....... ઉકેલ મળે.
ના ....... ઉકેલ મળે.
0
1
2
3
0
સમગુણોત્તર
 હોય, તો
હોય, તો 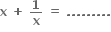
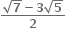
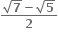
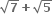

 અને
અને 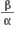 બીજ ધરાવતું દ્વિઘાત સમીકરણ ....... હોય.
બીજ ધરાવતું દ્વિઘાત સમીકરણ ....... હોય.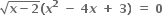 નાં વાસ્તવિક બીજ ...... હોય.
નાં વાસ્તવિક બીજ ...... હોય.
1,2,3
2, 3
1, 3
1, 2
 નું એક બીજ ....... હોય.
નું એક બીજ ....... હોય.
3
8
4
2