Book Store

Download books and chapters from book store.
Currently only available for.
CBSE

Gujarati JEE Mathematics : દ્વિઘાત સમીકરણ

Multiple Choice Questions

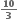21. જો log₂ x + log_x 2 = $begin inline style bold 10 over bold 3 end style$ = log₂y + log_y2 તથા x ≠ y હોય તો x+y = ......

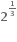
$bold 8 bold minus bold 2 to the power of begin inline style bold 1 over bold 3 end style end exponent$
$bold 2 to the power of begin inline style bold 1 over bold 3 end style end exponent$
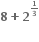
$bold 8 bold plus bold 2 to the power of begin inline style bold 1 over bold 3 end style end exponent$
8

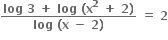22. સમીકરણ $fraction numerator bold log bold space bold 3 bold space bold plus bold space bold log bold space bold left parenthesis bold x to the power of bold 2 bold space bold plus bold space bold 2 bold right parenthesis over denominator bold log bold space bold left parenthesis bold x bold space bold minus bold space bold 2 bold right parenthesis end fraction bold space bold equals bold space bold 2$ ના ....... ઉકેલ મળે.

23.

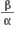જો α ≠ β તથા α² = 5α - 3 તેમજ β² = 5β - 3 હોય, તો $bold alpha over bold beta$ અને $bold beta over bold alpha$ બીજ ધરાવતું દ્વિઘાત સમીકરણ ....... હોય.

x² + 19x -3 = 0
3x² - 19x + 3 = 0
3x²-16x + 1 = 0
3x² -- 19x - 3 = 0

24. સમીકરણ $open parentheses bold 5 bold plus bold 2 square root of bold 6 close parentheses to the power of bold x bold minus bold 3 end exponent bold plus open parentheses bold 5 bold minus bold 2 square root of bold 6 close parentheses to the power of bold x bold minus bold 3 end exponent bold space bold equals bold space bold 10$ નું એક બીજ ....... હોય.

25.

જો દ્વિઘાત સમીકરણ (a² + b²)x² - 2b(a + c) x + (b²+c²)=0 નાં બીજ સમાન હોય તોa, b, c, ....... શ્રેણીમાં હોય a, b, c ∈ R.

સમગુણોત્તર
સમાંતર
સ્વરિત
સમાંતર-સમગુણોત્તર

26. જો x, y, z ભિન્ન અને વાસ્તવિક હોય, તો x² + 4y² + 9z² - 6yz - 3zx - 2xy હંમેશાં ....... હોય.

0
ઋણ
અનૃણ
સંકર સંખ્યા

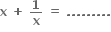
27. જો $bold x bold space bold equals bold space square root of bold 12 bold minus square root of bold 140 end root$ હોય, તો $bold x bold space bold plus bold space bold 1 over bold x bold space bold equals bold space bold. bold. bold. bold. bold. bold. bold. bold. bold.$

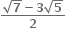
$fraction numerator square root of bold 7 bold minus bold 3 square root of bold 5 over denominator bold 2 end fraction$
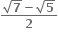
$fraction numerator square root of bold 7 bold minus square root of bold 5 over denominator bold 2 end fraction$
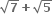
$square root of bold 7 bold plus square root of bold 5$
$fraction numerator bold 3 square root of bold 7 bold minus square root of bold 5 over denominator bold 2 end fraction$

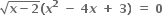28. સમીકરણ $square root of bold x bold minus bold 2 end root bold left parenthesis bold italic x to the power of bold 2 bold space bold minus bold space bold 4 bold italic x bold space bold plus bold space bold 3 bold right parenthesis bold space bold equals bold space bold 0$ નાં વાસ્તવિક બીજ ...... હોય.

1,2,3
2, 3
1, 3
1, 2

29.

જો 3,3 એ દ્વિઘાત સમીકરણ x² + ax + β = 0 નાં બીજ હોય તથા -8, 2 એ દ્વિઘાત સમીકરણ x² + αx + b = 0 નાં બીજ હોય, તો સમીકરણ x² + ax + b = 0 નાં બીજ ...... હોય.

-8, 2
8, -2
-2, -8
2, 8

8, -2

Tips: -

સમીકરણ x² + ax + β = 0 નાં બીજ 3, 3 હોવાથી, બીજનો સરવાળો 3 + 3 = -a આથી a = -6 મળે.

વળી, દ્વિઘાત સમીકરણ x² + ax + b = 0 નાં બીજ -8 તથા 2 છે. આથી બીજનો ગુણાકાર = -8 (2) = b

આથી b = -16.

આથી નવું દ્વિઘાત સમીકરકણ x² - 6x - 16 = 0 મળે.

∴ (x - 8) (x + 2) = 0

∴ x = 8 અથવા x = -2 મળે.

30.

દ્વિઘાત સમીકરણનો ઉકેલ શોધતી વખતે બે વિદ્યાર્થીઓ પૈકી એક વિદ્યાર્થી સમીકરણનું અચળ પદ ખોટું લખે છે અને સમીકરણનાં સાચાં બીજનો સરવાળો 3 મળે છે જ્યારે બીજો વિદ્યાર્થી x² નો સહગુણક તથા અચળ પદ સાચાં લખે છે જે અનુક્રમે 1 તથા -18 છે તો મળતા દ્વિઘાત સમીકરણનાં સાચાં બીજ ...... હોય.

-6, 3
6, -3
-3, -6
3, 6

Switch

Book Store

Subject

Gujarati JEE Mathematics : દ્વિઘાત સમીકરણ

Multiple Choice Questions

Switch