Book Store

Download books and chapters from book store.
Currently only available for.
CBSE

Gujarati JEE Mathematics : દ્વિઘાત સમીકરણ

Multiple Choice Questions

51.

જો p, q, r ધન હોય અને સમાંતર શ્રેણીમાં હોય, તો દ્વિઘાત સમીકરણ px² + qx + r = 0 નાં બીજ વાસ્તવિક હોવા માટે ......... હોવું જોઈએ.

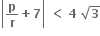
$open vertical bar bold p over bold r bold plus bold 7 close vertical bar bold space bold less than bold space bold 4 bold space square root of bold 3$
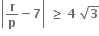
$open vertical bar bold r over bold p bold minus bold 7 close vertical bar bold space bold greater or equal than bold space bold 4 bold space square root of bold 3$
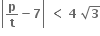
$open vertical bar bold p over bold t bold minus bold 7 close vertical bar bold space bold less than bold space bold 4 bold space square root of bold 3$
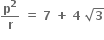
$bold p to the power of bold 2 over bold r bold space bold equals bold space bold 7 bold space bold plus bold space bold 4 bold space square root of bold 3$

52.

જો દ્વિઘાત સમીકરણ x² + x + 1 = 0 નાં બીજ α અને β હોય, તો જેનાં બીજ α¹⁹તથા β⁷ હોય તેવું દ્વિઘાત સમીકરણ ........ હોય.

x² + x - 1 = 0
x² - x + 1 = 0
x² + x + 1 = 0
x² - x - 1 = 0

53. જો દ્વિઘાત સમીકરણ x²-bx + c = 0 નાં બીજ બે ક્રમિક પૂર્ણાંકો હોય, તો b² - ac = .......

3
1
2
-2

54. દ્વિઘાત સમીકરણ x² + px + 8 = 0 ના બે બીજ વચ્ચેનો તફાવત 2 હોય, તો p ની કિંમત ..... હોય.

55. સમીકરણ x² + px + q = 0; p; q ∈ R નું એક બીજ 2 + $square root of bold 3 bold italic i$ હોય તો p = .......; q = ..........

p = 4, q = 7
p = 4, q = -7
p = -4, q = -7
p = -4, q = 7

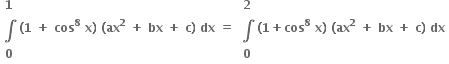56. શૂન્યેતર વાસ્તવિક સંખ્યાઓ a, b, c એવી મળે કે જેથી $table row bold 1 row bold integral row bold 0 end table bold left parenthesis bold 1 bold space bold plus bold space bold cos to the power of bold 8 bold space bold x bold right parenthesis bold space bold left parenthesis bold ax to the power of bold 2 bold space bold plus bold space bold bx bold space bold plus bold space bold c bold right parenthesis bold space bold dx bold space bold equals bold space table row bold 2 row bold integral row bold 0 end table bold left parenthesis bold 1 bold plus bold cos to the power of bold 8 bold space bold x bold right parenthesis bold space bold left parenthesis bold ax to the power of bold 2 bold space bold plus bold space bold bx bold space bold plus bold space bold c bold right parenthesis bold space bold dx bold space$ હોય, તો દ્વિઘાત સમીકરણ ax² + bx + c = 0 ને ......... .

(0, 2) માં એક પણ બીજ ન હોય.
(0, 2) માં બે બીજ હોય.
(1, 2) માં ઓછામાં ઓછું એકબીજ હોય જ.
બે વાસ્તવિક સંકર બીજ હોય.

(1, 2) માં ઓછામાં ઓછું એકબીજ હોય જ.

Tips: -

ધારો કે વિધેય,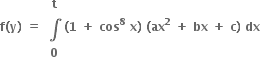 $bold f bold left parenthesis bold y bold right parenthesis bold space bold equals bold space table row bold t row bold integral row bold 0 end table bold left parenthesis bold 1 bold space bold plus bold space bold cos to the power of bold 8 bold space bold x bold right parenthesis bold space bold left parenthesis bold ax to the power of bold 2 bold space bold plus bold space bold bx bold space bold plus bold space bold c bold right parenthesis bold space bold dx$ છે.

વિધેય f [1, 2] પર સતત તથા (1, 2) પર વિકલનીય હોય છે જ. વળી f(1) = f(2)

આથી, સેલના પ્રમેય પરથી કોઈ k ∈ (1, 2) એવો મળે જ કે જેથી f'(k) = 0 થાય.

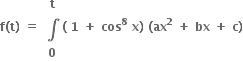
હવે, $bold f bold left parenthesis bold t bold right parenthesis bold space bold equals bold space table row bold t row bold integral row bold 0 end table bold left parenthesis bold space bold 1 bold space bold plus bold space bold cos to the power of bold 8 bold space bold x bold right parenthesis bold space bold left parenthesis bold ax to the power of bold 2 bold space bold plus bold space bold bx bold space bold plus bold space bold c bold right parenthesis$

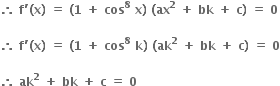
$bold therefore bold space bold f bold apostrophe bold left parenthesis bold x bold right parenthesis bold space bold equals bold space bold left parenthesis bold 1 bold space bold plus bold space bold cos to the power of bold 8 bold space bold x bold right parenthesis bold space bold left parenthesis bold ax to the power of bold 2 bold space bold plus bold space bold bk bold space bold plus bold space bold c bold right parenthesis bold space bold equals bold space bold 0 bold therefore bold space bold f bold apostrophe bold left parenthesis bold x bold right parenthesis bold space bold equals bold space bold left parenthesis bold 1 bold space bold plus bold space bold cos to the power of bold 8 bold space bold k bold right parenthesis bold space bold left parenthesis bold ak to the power of bold 2 bold space bold plus bold space bold bk bold space bold plus bold space bold c bold right parenthesis bold space bold equals bold space bold 0 bold therefore bold space bold ak to the power of bold 2 bold space bold plus bold space bold bk bold space bold plus bold space bold c bold space bold equals bold space bold 0$

∴ k એ દ્વિઘાત સમીકરણ ax² + bx + c = 0 નું એક બીજ થાય.

પરંતુ k ∈ (1, 2) હોવાથી, દ્વિઘાત સમીકરણ ax² + bx + c = 0 ને (1, 2) માં ઓછામાં ઓછું એક બીજ હોય જ.

57.

બે દ્વિઘાત સમીકરણો a₁x² + b₁x + c₁ = 0 અને a₂x² + b₂x + c₂ = 0 ને એક બીજ સામાન્ય(સમાન) હોય તો (a₁ b₂ - a₂ b₁) (b₁c₂ - b₂ c₁) ની કિંમત ....... હોય.

(a₁c₂-a₂c₁)²
(a₁c₁-a₂c₂)²
(a₁a₂-c₁c₂)²
-(a₁c₂-a₂c₁)²

58.

જો દ્વિઘાત સમીકરણ a (b - c)x² + b (c-a) x + c (a-b) = 0 નાં બે બીજ સમાન હોય તો a, b, c ........ શ્રેણીમાં હોય.

સમાંતર
સમગુણોત્તર
સમાંતર-સમગુણોત્તર
સ્વરિત

59. k ની ..... કિંમત માટે દ્વિઘાત સમીકરણ kx² + 1 = kx + 3x - 11x² નાં બીજ વાસ્તવિક તથા સમાન હોય.

5, -7
7, -5
5, 7
-11,-3

60. દ્વિઘાત સમીકરણ 3x² + 2x + p (-1)=0 નાં બીજ વિષમચિહન હોય તો p ની કિંમતોનો ગણ .....

(-∞, 0)
(1, ∞)
(0, ∞)
(0, 1)

Switch

Book Store

Subject

Gujarati JEE Mathematics : દ્વિઘાત સમીકરણ

Multiple Choice Questions

Switch