CBSE
 Multiple Choice Questions
Multiple Choice Questions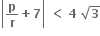
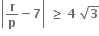
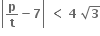
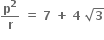
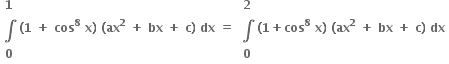 હોય, તો દ્વિઘાત સમીકરણ ax2 + bx + c = 0 ને ......... .
હોય, તો દ્વિઘાત સમીકરણ ax2 + bx + c = 0 ને ......... .
3
1
2
-2
A.
(a1c2-a2c1)2Tips: -
ધારૂ કે સમીકરણો a1x2 + b1x + c1 = 0 અને a2x2 + b2x + c2 = 0 નું એક સામાન્ય બીજ α છે.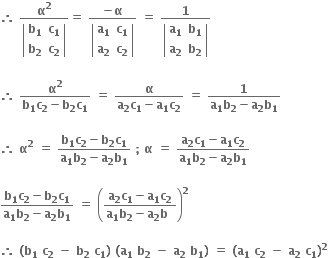
સમાંતર
 હોય તો p = .......; q = ..........
હોય તો p = .......; q = ..........