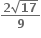CBSE
 Multiple Choice Questions
Multiple Choice Questions માટે
માટે 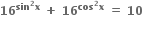 હોય તો x = .......... .
હોય તો x = .......... .
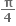

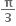

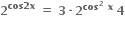 હોય તો x = ....... જ્યાં x ∈ [0,
હોય તો x = ....... જ્યાં x ∈ [0, ]
]

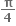
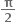
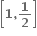
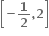
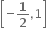
B.
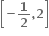
Tips: -
a2 + b2 + c2 = 1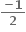 ≤ (ab + bc + ca)
≤ (ab + bc + ca) 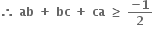
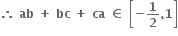 અથવા
અથવા 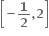 હોઈ શકે.
હોઈ શકે.
માત્ર એક જ કાલ્પનિક બીજ થાય.
 હોય તો x3 - 6x2 + 6x ની કિંમત ....... હોય.
હોય તો x3 - 6x2 + 6x ની કિંમત ....... હોય.
3
1
2
2/3
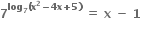 હોય તો x ની શક્ય કિંમતો ..... હોય.
હોય તો x ની શક્ય કિંમતો ..... હોય.
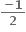
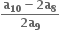
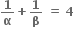 હોય તો |α -β| = ........ .
હોય તો |α -β| = ........ .