CBSE
 Multiple Choice Questions
Multiple Choice Questions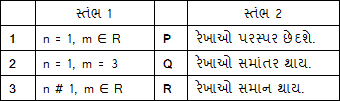
(1)→(R), (2)→(p), (3)→(Q)
(1)→(Q), (2)→(R), (3)→(P)
(1)→(R), (2)→(Q), (3)→(P)
(1)→(Q), (2)→(P), (3)→(R)
જો 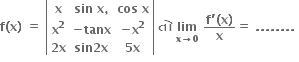
0
1
2
4
આપેલી સમીકરણોની સંહતિ માટે અને λ મેળવો μ તથા નીચેના સ્તંભોમાં યોગ્ય જોડી રચો :
x + 2y + 3z = 6, x + 3y + 5z = 9, 2x + 5y + λz = μ
(1)→(R), (2)→(Q), (3)→(P)
(1)→(P), (2)→(Q), (3)→(R)
(1)→(Q), (2)→(R), (3)→(P)
(1)→(R), (2)→(P), (3)→(Q)
C.
(1)→(Q), (2)→(R), (3)→(P)
Tips: -
x + 2y + 3z = 6 ... (1)
x + 3y + 5z = 9 ... (2)
2x + 5y + λz = μ ... (3)
સમીકરણ (1) ને 2 વડે ગુણીને સમીકરણ (3) માંથી બાદ કરતાં,
y + (λ - 6)z = μ - 12 ... (4)
સમીકરણ (2) ને 2 વડે ગુણીને સમીકરણ (3) માંથી બાદ કરતાં,
-y + (λ - 10)z = μ - 18 ... (5)
સમીકરણ (4) અને (5) નો સરવાળો કરતાં,
(2λ - 16)z = 2μ - 30
(λ - 8z = μ - 15
λ # 8 અને μ R માટે અનન્ય ઉકેલ મળે. (2)→(R)
λ = 8 અને μ = 15 માટે ઉકેલ મળે નહિ. (1)→(Q)
λ =8 અને μ = 15 માટે ઉકેલ મળે. (3)→(P)
[નોંધ : નિશ્ચાયક લઈને પોઅણ ગણી શકાય.]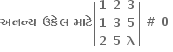
3-25-2(λ-10)-3 # 0
λ # 8
હવે માત્ર વિકલ્પ જવાબ (B) બને.