CBSE
 Multiple Choice Questions
Multiple Choice Questionsજો xm yn = (x + y)m+n તો 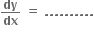

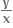
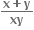
xy
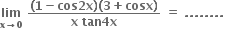
4
3
2
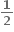
જો f(x) = (1 + x)n, તો f(0) + f(0) +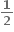 fn(0) + ..... +
fn(0) + ..... +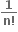 fn(0) = ......
fn(0) = ......
n
1
2n
2n-1
a આગળ સતત નથી.
a આગળ સતત હોય.
a આગળ વિકલનીય હોય.
0 આગળ વિકલનીય હોય.
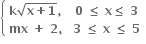 વિકલનીય હોય, તો k + m = ........
વિકલનીય હોય, તો k + m = ........
2
4
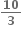
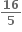
A.
2
Tips: -
જો g(x) = વિકલનીય હોય, તો g એ x = 3 આગળ સતત પણ હોય.
∴  g(x) = g(3)
g(x) = g(3)
∴3m + 2 = 2k
g(x) વિકલનીય છે. ∴ g'(3+) = g'(3-)
∴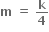 . આથી k = 4m આથી 3m + 2 = 8m
. આથી k = 4m આથી 3m + 2 = 8m 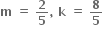 . આથી k + m = 2
. આથી k + m = 2
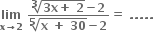
10
20
30
40
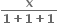 વિકલનીય થશે ?
વિકલનીય થશે ?
(-∞, ∞)
(0, ∞)
(-∞, 0) ∪ (0, ∞)
(-∞, -1) ∪ (-1, ∞)
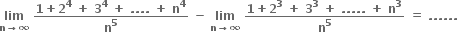
0


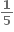
2
3
5
6
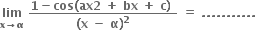
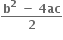
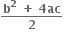
1
0