CBSE
 Multiple Choice Questions
Multiple Choice Questions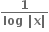 એ કેટલાં બિંદુઓએ અસતત થશે ?
એ કેટલાં બિંદુઓએ અસતત થશે ?
1
2
3
4
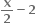 તો અંતરાલ
તો અંતરાલ 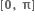 પર
પર
tan (f(x)) અને f-1(x) બંને સતત થશે.
tan (f(x)) અને f-1(x) બંને અસતત થશે.
tan (f(x)) અને  બંને સતત થશે.
બંને સતત થશે.
tan (f(x)) અને  બંને અસતત થશે.
બંને અસતત થશે.
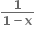 g(x) = f3n(x) જ્યાં fn(x) = fofof ..... of (n વખત). વિધેય g(x) કેટલા બિંદુએ અસતત થશે ?
g(x) = f3n(x) જ્યાં fn(x) = fofof ..... of (n વખત). વિધેય g(x) કેટલા બિંદુએ અસતત થશે ? 2ન
3n
2
2n + 1
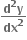 = ........
= ........
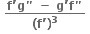
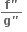
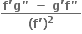
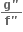
n
1 - n2
1 + n2
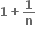
C.
1 + n2
Tips: -
 -b sin (log x)
-b sin (log x) )
)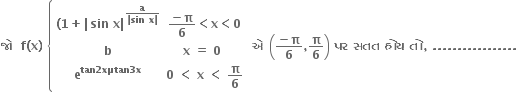
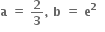
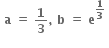
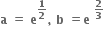
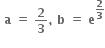
f અને g વિકલનીય વિધેય છે. g'(a) = 2. g(a) = b તથા fog = I તો f'(b) = ........
1
2
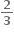
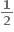
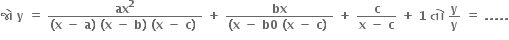
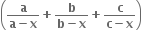
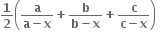
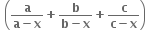

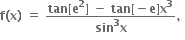 x # 0. જો f એ x = 0 આગળ સતત હોય તો f(0) = .....
x # 0. જો f એ x = 0 આગળ સતત હોય તો f(0) = .....12
-12
14
15
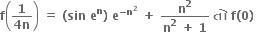 ની કિંમત .....
ની કિંમત ..... 0
-1
1