CBSE
 Multiple Choice Questions
Multiple Choice Questionsf એ R પર સતત નથી.
f(x) એ અમુક બિંદું સિવાય વિકલનીય છે.
f(x) એ (a, b)જ્યાં a < 0 < b અંતરાલમાં વિકલનીય હોય.
f(x) = અચળ
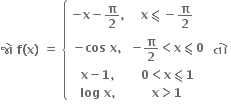
f(x) એ x =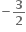 , 1આગળ વિકલનીય છે.
, 1આગળ વિકલનીય છે.
f(x) એ x =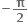 આગળ સતત છે.
આગળ સતત છે.
f(x) એ x = 0 આગળ વિકલનીય નથી.
આપેલ તમામ
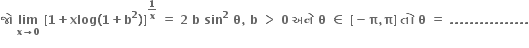
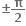
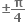
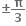
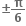
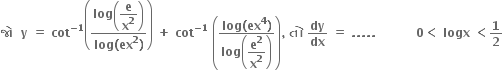
1
-1
2
0
1
-1
2
0
એક ઉકેલ મળે.
ઉકેલ નથી.
બે ઉકેલ મળે.
ઓછામાં ઓછા ત્રણ ઉકેલ મળે.
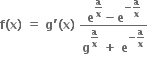 જ્યાં g' એ વિધેય g નું વિકલિત છે તથા સતત વિધેય છે અને a > 0. જો
જ્યાં g' એ વિધેય g નું વિકલિત છે તથા સતત વિધેય છે અને a > 0. જો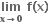 નું અસ્તિત્વ હય તો
નું અસ્તિત્વ હય તો g(x) = a0 + a1x + a2x2 + ..... + anx-n જ્યાં ai ∈ R, i = 1,2 ....n તથા a1 # 0 an # 0
g(x) = log (1 + x)
g એવું વિધેય હોય જ્યાં g'(0) = 0
g(x0 = sin x
 x, વિધેયનું fનું x = k,k ∈ Z આગળ ડાબી બાજુનું વિકલિત ...... છે.
x, વિધેયનું fનું x = k,k ∈ Z આગળ ડાબી બાજુનું વિકલિત ...... છે. (-1)k-1 (k-1) 
(-1)k k
(-1)k-1 k
(-1)k (k -1)
|f'(x)| > 1
|f'(x)|>1
|f''(x)| < 1
|f(x)|<1
C.
|f''(x)| < 1
Tips: -
f(0) = f(1) હોવાથી રોલના પ્રમેયની મદદથી એવો c, 0 < c < 1 માં મળે કે જેથી f'(c) = 0
ધારો કે (0, 1) માં c સિવાયનું બિંદું x છે. અંતરાલ (x, c) માં f' માટે લાગ્રાન્જના પ્રમેયનો ઉપયોગ કરતા
f'(x) - f'(c) = (x-c) f"(c1)(x<c1<c)
|f'(x)| = |x - c| |f"(c1)|<1 (|x - c| , 1| (|x-c| , |f"(c1)|≤1)
|f'(x) |<1
નોંધ : [c, x] માં પણ આ રીતે સાબિત થાય છે.
f(x) = [x] + [-x]
f(x) = |x| [x]
f(x) = |x| - |sin x|