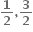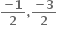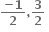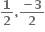CBSE
 Multiple Choice Questions
Multiple Choice Questions
∉R
R-
R+
{0}
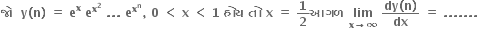
4e
3e
2e
e
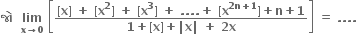
1
-1
0
લક્ષનું અસ્તિત્વ નથી.
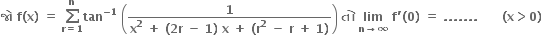
e
-1
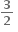
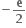
f'(1) = 0
af'(1) < 0
af'(1) > 0
af'(1) વિશે કઈ તારણ ન મળે.
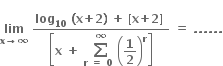 જ્યાં [•] એ મહત્તમ પૂર્ણાંક ભાગ વિધેય છે.
જ્યાં [•] એ મહત્તમ પૂર્ણાંક ભાગ વિધેય છે. 1
-1
0
લક્ષનું અસ્તિત્વ નથી.
કોઈક x ∈(2, 4) માટે g'(x) = 4f'(x)
g'(x) > 4 f'(x), ∀x ∈(2, 4)
A.
કોઈક x ∈(2, 4) માટે g'(x) = 4f'(x)
Tips: -
ધારો કે, h(x) = g(x) - 4f(x)
h(2) = g(4) - 4 f(2) = 0 - 4.8 = -32
h(4) = g(4) - 4f(40 = 8 -4.10 = -32
વળી, h એ [2, 4] પર સતત છે તથા (2, 4) પર વિકલિત છે.
વિધેય h એ રોલના પ્રમેયની શરતનું સમાધાન કરે છે.
કોઈક x ∈(2, 4) માટે h'(x) = 0
g'(x) = 4 f'(x)
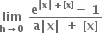 નું અસ્તિત્વ ન હોય, તો a = ......
નું અસ્તિત્વ ન હોય, તો a = ......
1 + e
(1 - e-1)-1
1 - e-1
0
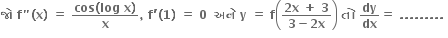

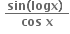

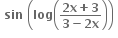
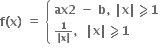 એ x = 1 આગળ વિકલનીય હોય, તો a = ....... , b = ..........
એ x = 1 આગળ વિકલનીય હોય, તો a = ....... , b = ..........