CBSE
 Multiple Choice Questions
Multiple Choice Questionsત્રણે બીજ ઋણ હોય.
ત્રણે બીજ ધન હોય.
એક ઋણ, બે ધન હોય.
બે અવાસ્તવિક સંકર સંખ્યા હોય.
B.
ત્રણે બીજ ધન હોય.
Tips: -
f(x) = (x - 1) (x - 2) (x - 3) (x - 4)
અંતરાલ [1,2]. [2, 3], [3, 4] પર રોલના પ્રમેયનો ઉપયોગ કરતા f'(x) ને (1, 2), (2, 3), (3, 4) માં એક-એક બીજ મળે.
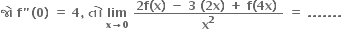
-6
6
-12
12
f: [0,4] → R એ વિકલનીય વિધેય છે. જો અંતરાલ (0, 4) માં a, b એવા મળે કે જેથી
(f(4)2 - f(0))2 = k f'(a) f(b) તો k = .....
1
4
8
શક્ય નથી.
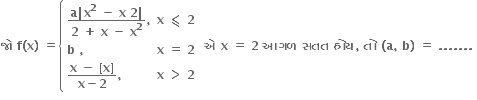
(1, 1)
(1, 2)
(2, 1)
(2, 2)
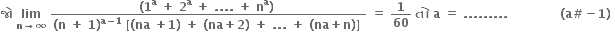
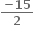
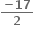
5
7
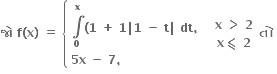
f એ x = 2 આગળ સતત છે પરંતુ વિકલનીય નથી.
f એ x = 2 આગળ સતત નથી
f એ R પર વિકલનીય છે.
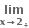 f(x) નું અસ્તિત્વ નથી
f(x) નું અસ્તિત્વ નથી
f(6)≥8
f(6) = 5
f(6)< 5
f(6)<2
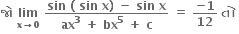
a = -2, b ∈ R, c = 0
a = 1, b ∈ R, c = 0
a = -1, B ∈ R, c = 0
a = 2, b ∈ R, c = 0
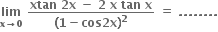
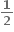
-1
2
-2
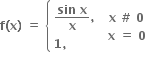
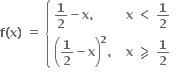
f(x) |x|
f(x) = x |x|