CBSE
 Multiple Choice Questions
Multiple Choice Questions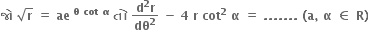
0
1

r


e
1
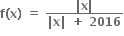 એ કેટલા બિંદુએ વિકલનીય નથી ?
એ કેટલા બિંદુએ વિકલનીય નથી ?
0
1
2
અનંત
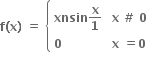 જો f(x) એ x = 0 આગળ સતત હોય, પરંતુ વિકલનીય ન હોય તો
જો f(x) એ x = 0 આગળ સતત હોય, પરંતુ વિકલનીય ન હોય તો n = 0
n∈(0,1]
n∈[1, ∞)
n∈(-∞, 0)
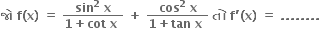
sin 2x
-sin 2x
cos 2x
-cos 2x
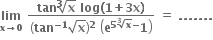
0
1


જો f(x + y + z) = f(x) f(y) f(z), ∀x, y ∈ R, f(4) = 4, f(0) = 2 તો f'(4), f(4), f(0) એ ....
આપેલ તમામ સત્ય છે.
સમાંતર શ્રેણીમાં છે.
સમગુણોત્તર શ્રેણીમાં છે.
સ્વરિત શ્રેણીમાં છે.
જો xy = e - ey તો 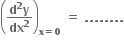
e2



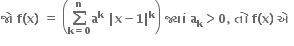
R પર વિકલનીય છે.
R પર સતત છે. પરંતુ x = 1 આગળ વિકલનીય નથી.
x = 1 આગળ સતત નથી.
R પર સતત છે, પરંતુ x = 0 આગળ વિકલનીય નથી.
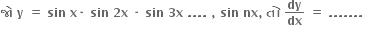
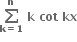

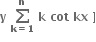

C.
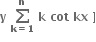
Tips: -
y = sin x • sin 2x • sin 3x • ...... • sin x
∴ log y = log sin x + log sin 2x + ... + log sin nx 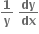 = cot x + 2 cot 2x + ..... + n cot nx
= cot x + 2 cot 2x + ..... + n cot nx