CBSE
 Multiple Choice Questions
Multiple Choice Questions
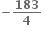
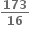
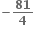
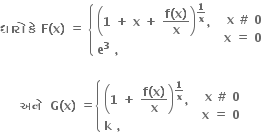
1
2
3
0
એક વાસ્તવિક બીજ મળે.
બે વાસ્તવિક બીજ મળે.
આઠ વાસ્તવિક બીજ મળે.
અનંત ઉકેલો મળે.
વક્ર y2 - x2 = 1 પર બિંદુ P એવું છે કે જેનો x યામ n હોય, જ્યાં n ∈ N. જો dn એ બિંદુ Pરેખા y = x પરનું અંતર દર્શાવે, તો  = .......
= .......
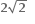
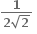
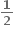
1
2
4
6
8
1:2
1:3
2:1
4:1
C.
2:1
Tips: -
ધારો કે વર્તુળની ત્રિજ્યા r અને ચોરસની પરિમિતિનો સરવાળો 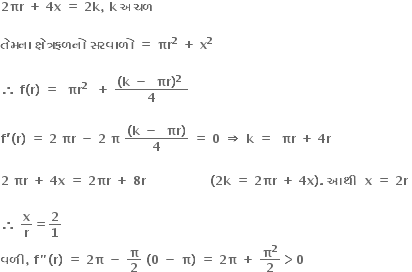
ચોરસની બાજુ તથા વર્તુળની ત્રિજ્યાનો ગુણોત્તર 2:1 હોય ત્યારે ક્ષેત્રફળનો સરવાળો ન્યુનતમ છે.
f(y) < x
f(y) < x
f(y) = x
f(y) > x
tan x = x, cot x = x
sin x = x, tan x = x
cot x =x, sec x = x
cot x = x, tan x = x
-a
a
-1
1
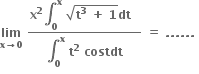
1
2
3
0