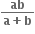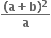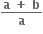CBSE
 Multiple Choice Questions
Multiple Choice Questions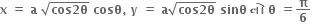 આગળનો સ્પર્શક .........
આગળનો સ્પર્શક ......... રેખા y = x ને સમાંતર છે.
રેખા x + y = 1 ને સમાંતર છે.
X-અક્ષને સમાંતર છે.
Y-અક્ષને સમાંતર છે.
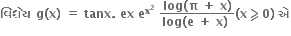
 પર વધતું તથા
પર વધતું તથા 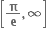 પર ઘટતું વિધેય છે.
પર ઘટતું વિધેય છે.
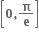 પર ઘટતું તથા
પર ઘટતું તથા 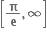 પર વધતું વિધેય છે.
પર વધતું વિધેય છે.
[0, ∞]પર વધતું વિધેય છે.
[0, ∞]પર ઘટતું વિધેય છે.
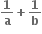
જો f(x)= અને g(x) = , 0<x<1, તો આ અંતરાલમાં
f(x) વધતું વિધેય છે અને g(x) ઘટતું વિધેય છે.
g(x) વધતું વિધેય છે અને f(x) ઘટતું વિધેય છે.
f(x) અને g(x) બંને વધતાં વિધેય છે.
f(x) અને g(x) બંને ઘટતાં વિધેય છે.
(0, 2)
(0, -2)
(0, 1)
(0, -1)
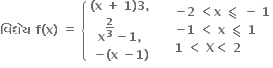
1
2
3
4
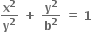 પર P કોઈ એક બિંદુ છે. કેન્દ્ર 0 માંથી દોરેલ P પરના સ્પર્શક પર દોરેલ લંબનો લંબપાદ N છે. ધારો કે Amax એ ∆OPN નું મહત્તમ ક્ષેત્રફળ છે.
પર P કોઈ એક બિંદુ છે. કેન્દ્ર 0 માંથી દોરેલ P પરના સ્પર્શક પર દોરેલ લંબનો લંબપાદ N છે. ધારો કે Amax એ ∆OPN નું મહત્તમ ક્ષેત્રફળ છે. 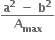 ની કિંમત .....
ની કિંમત ..... 1
2
4
8
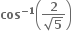
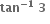
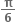
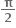
નીચેનામાંથી કયા અંતરાલમાં a ની કિંમત આવે તો
f(x) = sinx - asin2x -  sinx3 + 2ax એ R પર વધતું વિધેય થાય ?
sinx3 + 2ax એ R પર વધતું વિધેય થાય ?
[0, ∞)
[1, ∞)
[0, ∞)
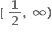
B.
[1, ∞)
Tips: -
f(x) = cosx - 2acos2x - cos3x + 2a
cosx - 2a(2cos2x - 1) - (4cos3x - 3cosx) + 2a
4a + 4cosx - 2acos2x - 4cos3x
4asin2x + 4cosxsin2x
4sin2x (a + cosx)
-1 ≤ cosx≤ 1 ⇒ a - 1 ≤ a + cosx ≤ a + 1 જો a ≥ 1 હોય તો, f(x) ≥ 0 થાય.
જો f એ R પર વધતું વિધેય હોય, તે માટે a ∈[1, ∞] પર્યાપ્ત છે.
2
-3
4
5
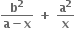 , 0 < x < a નું ન્યુનતમ મૂલ્ય ...... થાય.
, 0 < x < a નું ન્યુનતમ મૂલ્ય ...... થાય.