CBSE
 Multiple Choice Questions
Multiple Choice Questionsવધતું વિધેય છે.
ઘટતું વિધેય છે.
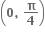 માં વધતું તથા
માં વધતું તથા 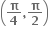 માં ઘટતું વિધેય છે.
માં ઘટતું વિધેય છે.
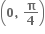 માં ઘટતું તથા
માં ઘટતું તથા 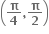 માં વધતું વિધેય છે.
માં વધતું વિધેય છે.
 2(x - k) ને x ની કઈ કિંમત માટે ન્યુનત્તમ મળે ?
2(x - k) ને x ની કઈ કિંમત માટે ન્યુનત્તમ મળે ?
0
1000
1008
2015
જો f વધતું વિધેય હોય, તો અનુક્રમે h પણ વધતુ કે ઘટતું વિધેય થાય.
જો f ઘટતું વિધેય હોય, તો h વધતું વિધેય છે.
જો f વધતું વિધેય હોય, તો h વધતુ વિધેય છે.
h વિશે કઈ કહી શકાય નહિ.
a = કયા ગણનો સભ્ય હોય તો વિધેય 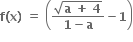 x5 - 3x + log5 એ R પર ઘટતું વિધેય થશે ?
x5 - 3x + log5 એ R પર ઘટતું વિધેય થશે ?
(-∞, ∞)
(1, ∞)

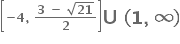
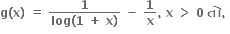
-∞ < g(x) < 0
0 < g(x) < 1
1 < g(x) < 2
-1 < g(x) < 0
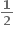 cos 2x -
cos 2x - cos 3x નાં મહત્તમ તથા ન્યુનત્તમ મૂલ્યો વચ્ચેનો તફાવત ..... છે.
cos 3x નાં મહત્તમ તથા ન્યુનત્તમ મૂલ્યો વચ્ચેનો તફાવત ..... છે. 


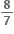
A.

Tips: -
આપેલ વિધેય f(x)નું મુખ્ય આવર્તમાન  હોવાથી આપણે માંગેલ તફાવત
હોવાથી આપણે માંગેલ તફાવત 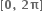 માં શોધીશું.
માં શોધીશું.
f'(x) = -(sina x + sin 2x - sin 3x)
= - sin x + sin 3x - sin 2x 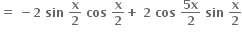

= - 4 sin x sin 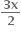 sin
sin
∴ x = 0,  એ વિવેચક બિંદુ છે.
એ વિવેચક બિંદુ છે.
વળી, 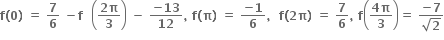
∴ માંગેલ તફાવત = 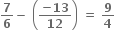
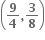
(4,4)
(-1,2)
(-1, -1)
16
28
30
31
24
2
3
4
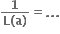
12
9
6
3