CBSE
 Multiple Choice Questions
Multiple Choice Questions
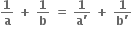
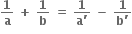
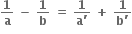
સ્વરિત શ્રેણીમાં હોય.
સમાંતર તેમજ સમગુણોત્તર શ્રેણીમાં હોય.
સમગુણોત્તર શ્રેણીમાં હોય.
સમાંતર શ્રેણીમાં હોય.
C.
સમગુણોત્તર શ્રેણીમાં હોય.
Tips: -
y = x3 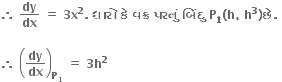
P1 આગળ સ્પર્શકનું સમીકરણ, y - h3 = 3h2(x - h)
∴(x - h) x2 + xh + h2) = 3h2(x - h) (વક્ર સાથેના છેદબિંદુ આગળ)
∴ x2 + xh - 2h2 = 0 અથવા x = h
∴ (x - h) (x + 2h) = 0
∴ x = -h. આથી y = -8h3
∴ P2(-2h, -8h3)
∴ P3 નો x યામ -2(-2h) = 4h તથા y યામ 64 h3
∴ P3 = (4h, 64h3)
આ જ રીતે આગળ વધતાં જોઈ શકાય છે કે, P1, P2, P3, ...... Pn ના X - યામ h, -2h, 4h, ..... એ સમગુણોત્તર શ્રેણીમાં છે.
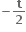
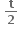
2t
-t

3Q = 4P
3P = 4Q
p = 2Q = 5
2(P + Q) = 7
જો વક્ર xy + ax + by = 0 નો (1,1) આગળનો સ્પર્શક X-અક્ષ સાથે tan-1 2 માપનો ખૂણો બનાવે તો (a, b)
(1, 2)
(1, -2)
(-1, -2)
(-1, 2)
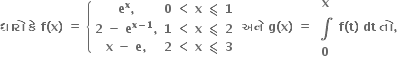
x = 1 આગળ g ને સ્થાનીય મહત્તમ તથા x = 2 આગળ g ને સ્થાનીય ન્યુનત્તમ મૂલ્ય મળે છે.
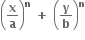 = 2 એ રેખા
= 2 એ રેખા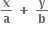 = 2 ને સ્પર્શે તો n = ......
= 2 ને સ્પર્શે તો n = ......
માત્ર 2
માત્ર 3
માત્ર 4
કોઈપણ શુન્યેત્તર વાસ્તવિક સંખ્યાં
(0, ∞) પર વધતું તથા (-∞, 0) પર ઘટતું વિધેય છે.
f વિશે કઈ શકાય નહિ.
R પર વધતું વિધેય છે.
R પર ઘટતું વિધેય છે.
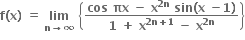
f એ x = 1 આગળ સતત છે.
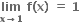

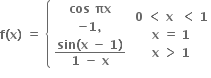
f(3) = 12
f એક-એક છે પરંતુ વ્યપ્ત નથી.
f એક - એક અને વ્યાપ્ત છે.
f(x) = x ને ત્રણ ભિન્ન વાસ્તવિક ઉકેલ મળે.