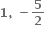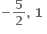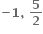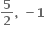CBSE
 Multiple Choice Questions
Multiple Choice Questions આગળનો સ્પર્શક જો વક્રને ફરીથી બિંદુ Q આગલ મળે, તો PQ = ......
આગળનો સ્પર્શક જો વક્રને ફરીથી બિંદુ Q આગલ મળે, તો PQ = ...... 

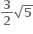
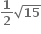
C.
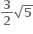
Tips: -
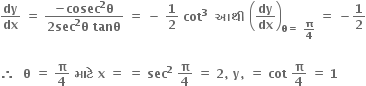
∴ વક્ર પરનું બિંદુ, બિંદુ P(2,1) થશે.
P આગળ સ્પર્શકનું સમીકરણ, y - 1 =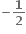 (x -2)
(x -2)
∴ x + 2y - 4 = 0 (1)
હવે, x = sec2θ, y = cot θ
sec2θ - tan2θ = 1 નો ઉપયોગ કરતાં θ નો લોપ કરી શકાય. 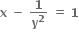
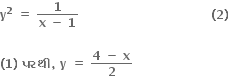
છેદ બિંદુ માટે, (2) માં મૂકતાં 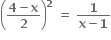
∴ (x2 - 8x + 16) (x - 1) = 4
∴ x3 - 9x2 + 24x - 20 = 0
∴ (x - 2)(x2 - 7x + 10) = 0
∴ (x - 2)2 (x - 5) = 0
∴ x = 2, 5
જો x = 2 તો y = 1. જો x = 5 તો 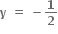
∴ P(2, 1) (જે આપેલ છે) તેથી Q =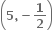
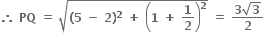
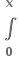 2|t|dt માટે પ્રથમ ચરણની દ્વિભજક રેખા એટૅલે કે y = x ને સમાંતર હોવાથી,
2|t|dt માટે પ્રથમ ચરણની દ્વિભજક રેખા એટૅલે કે y = x ને સમાંતર હોવાથી, 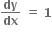
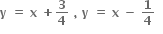
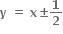

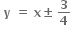
3a2
a2
4a2
2a2
3
-3
1
-1
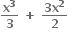 + ax + b. જો F(-2) = 0 હોય, તો એવી કેટલી ક્રમયુક્ત હોડ (a, b) શક્ય બને જ્યાં વિધેય F એ P(-2, 0) આગળ ન્યુનતમ હોય.
+ ax + b. જો F(-2) = 0 હોય, તો એવી કેટલી ક્રમયુક્ત હોડ (a, b) શક્ય બને જ્યાં વિધેય F એ P(-2, 0) આગળ ન્યુનતમ હોય. 1
2
3
0
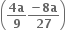
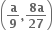
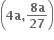
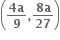
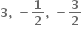
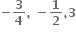
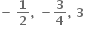
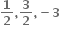
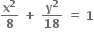 ના બિંદુ P (x, y) આગળનો સ્પર્શક અક્ષોને બિંદુ A તથા B માં છેદે છે. જો OAB નું ક્ષેત્રફળ ન્યુનતમ હોય તો બિંદુ P એ ......
ના બિંદુ P (x, y) આગળનો સ્પર્શક અક્ષોને બિંદુ A તથા B માં છેદે છે. જો OAB નું ક્ષેત્રફળ ન્યુનતમ હોય તો બિંદુ P એ ...... 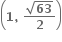
(2, 3)
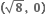
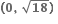
(-∞, 0) ∪ (3, ∞)
(0, 3)
(0, ∞)
(0, 1)