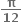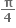CBSE
 Multiple Choice Questions
Multiple Choice Questions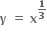 (1 - cos x) ને x = 0 આગળના સ્પર્શકનું સમીકરણ .... થશે.
(1 - cos x) ને x = 0 આગળના સ્પર્શકનું સમીકરણ .... થશે.
x = 0
x = 1
y = 0
y = 1
R

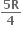

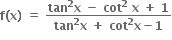 માટે નીચેનામાંથી કયા વિધાન સત્ય છે ?
માટે નીચેનામાંથી કયા વિધાન સત્ય છે ?
f(x)નું વૈશ્વિક ન્યુઅનતમ મૂલ્ય -1 છે.
f(x)નું વૈશ્વિક મહત્તમ મુલ્ય  છે.
છે.
f(x)ને વૈશ્વિક ન્યુનતમ મૂલ્ય ન મળે.
f(x)ને વૈશ્વિક મહતમ મૂલ્ય ન મળે.
0
2

(A) અથવા (c)
 માપનો ખુણો બનાવે છે તથા જે બિંદુના x - યામ અનુક્રમે 2 તથા 3 હોય તે બિંદુએ
માપનો ખુણો બનાવે છે તથા જે બિંદુના x - યામ અનુક્રમે 2 તથા 3 હોય તે બિંદુએ  તથા
તથા 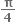 માપના ખૂણા બનાવે છે, તો
માપના ખૂણા બનાવે છે, તો 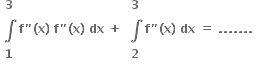
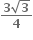
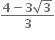
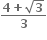
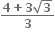
G(x) એ વધતું વિધેય છે.
G(x) એ ઘટતું વિધેય છે.
G(x) એ એક-એક વિધેય છે.
G(x) એ વધતું કે ઘટતું વિધેય નથી.
 ] માં કેટલા ઉકેલ મળે ?
] માં કેટલા ઉકેલ મળે ?
1
2
3
0
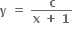 નો સ્પર્શક હોય, તો c = .......
નો સ્પર્શક હોય, તો c = .......
1
2
4
8
C.
4
Tips: -
બિંદુ (0, 3) અને (5, -2) માંથી પસાર થતી રેખા 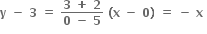
કોઈ બિંદુ આગળ સ્પર્શકનું સમીકરણ x + y - 3 = 0 છે.
બિંદુ(α, β) માટે, α + β - 3 = 0 (1) 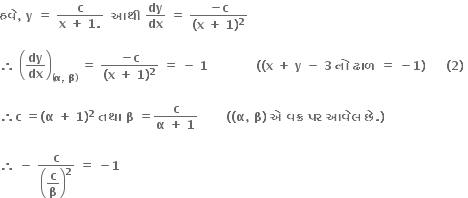
β2 = c અથવા (3 - α)2 = c = (α 1)2
3 - α = ± (α + 1)
3 - α = α + 1 આથી α = 1
c = (1 + 1)2 = 4
વિધેય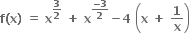 નું ન્યુનતમ મૂલ્ય ....... છે.
નું ન્યુનતમ મૂલ્ય ....... છે.
-10
10
0
ન મળે.
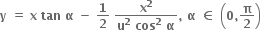 ના બિંદુ P આગળનો સ્પર્શક રેખા y = x + 5 ને સમાંતર છે. જો બિંદુ P નો y - યામ
ના બિંદુ P આગળનો સ્પર્શક રેખા y = x + 5 ને સમાંતર છે. જો બિંદુ P નો y - યામ  હોય તો α = ......
હોય તો α = ......