CBSE
 Multiple Choice Questions
Multiple Choice Questions(2, 7)
(-1, 2)
(0, 7)
[-7, 1]
 આગળ ન્યુનત્તમ હોય, તો નીચેનમાંથી કયું વિધાન સાચું છે.
આગળ ન્યુનત્તમ હોય, તો નીચેનમાંથી કયું વિધાન સાચું છે. 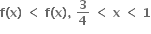
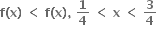
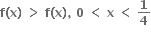
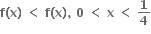
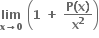 જો P(x) ને x = 1,2 આગળ મહત્તમ કે ન્યુનતમ અસ્તિત્વ ધરાવે તો P(2) = .......
જો P(x) ને x = 1,2 આગળ મહત્તમ કે ન્યુનતમ અસ્તિત્વ ધરાવે તો P(2) = ....... 1
2
3
0
 + f(1 - x) અને 0 ≤ x ≤ 1 માટે અને f"(x) 0 તો g(x) એ
+ f(1 - x) અને 0 ≤ x ≤ 1 માટે અને f"(x) 0 તો g(x) એ
 માં ઘટતું વિધેય છે.
માં ઘટતું વિધેય છે.
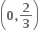 માં વધતું વિધેય છે.
માં વધતું વિધેય છે.
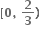 માં ઘટતું વિધેય છે.
માં ઘટતું વિધેય છે.
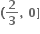 માં વધતું વિધેય છે.
માં વધતું વિધેય છે.
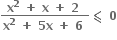 નું સમાધાન કરે તો પ્રચલ a ની કિંમત ...... ગણમાં હોય.
નું સમાધાન કરે તો પ્રચલ a ની કિંમત ...... ગણમાં હોય. 
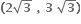
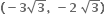

2y = x + 8
3y = 9x + 2
y = x + 2
y = 2x + 1
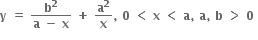 નું ન્યુનતમ મૂલ્ય ....... છે.
નું ન્યુનતમ મૂલ્ય ....... છે.
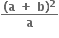
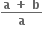
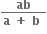
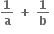
વિધેય f(x) = 2|x| + |x + 2| - 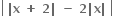 ને x ની કઈ કિંમત માટે સ્થાનિય મહત્તમ કે સ્થાનીય ન્યુનતમ મૂલ્ય મળે ?
ને x ની કઈ કિંમત માટે સ્થાનિય મહત્તમ કે સ્થાનીય ન્યુનતમ મૂલ્ય મળે ?
2

-2
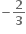
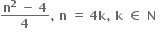
 યુગ્મ સંખ્યા હોય.
યુગ્મ સંખ્યા હોય.
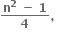 અયુગ્મ સંખ્યા હોય.
અયુગ્મ સંખ્યા હોય.
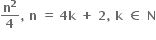
8
5
3
2
D.
2
Tips: -
અહીં, 4x2 + a2y2 + 4a2 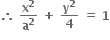
ધારો કે (u, v) = (a = cos θ, 2 sin θ) એ આપેલ વક્ર પરનું બિંદુ છે. (0, -2) થી અંતર
f(θ) = a2 cos2 θ + (2 sin θ + 2)2
f'(θ) = 0 ⇒ 2a2cosθ(-sin θ) + 8(sin θ + 1) cosθ = 0
∴ cos θ {(8 - 2a2) sin θ + 8} = 0 
હવે, 4 < a2 < 8
∴ 0 < a2 - 4 < 4. આથી 0<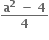 <1
<1 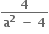 >1. પરંતુ sin θ ≤1 આથી θ =
>1. પરંતુ sin θ ≤1 આથી θ = 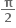
∴ વક્ર પરનું બિંદુ (0, 2) આથી u + v = 0 + 2 = 2