Gujarati JEE Mathematics : લક્ષ-સાતત્ય અને વિકલન

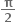
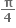
B.

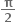
Tips: -

f(x)f(y) - f(xy) = x + y, ∀ x, y∈ R

x = 1, y = 1 લેતાં, (f(1))² - f(1) - 2 = 0

∴ (f(1) - 2) (f (1) + 1) = 0

વળી, f(1) > 0. આથી f(1) = 2

(1) માં y = 1 મૂકતાં, f(x) 2 - f(x) = x + 1

∴ f(x0 = x + 1 આથી f^-1(x) = x - 1

∴ h(x) = f(x)f^-1(x) = x² - 1

h(sin x + cos x) = (sin x + cos x)² - 1 = sin 2x

આપણે જાણીએ છીએ કે sin x ચુસ્ત રીતે વધતું હોય તેવા મોટામાં મોટા અંતરાલની લંબાઈ છે.

∴ sin 2x માટે માંગેલ અંતરાલની લંબાઈ 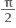 થાય.