CBSE
 Multiple Choice Questions
Multiple Choice QuestionsA
I-A
A+I
જો તો નીચે 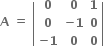 પૈકીનું કયું સત્ય છે ?
પૈકીનું કયું સત્ય છે ?
A2 = I
A શુન્ય શ્રેણિક છે.
A-1અસ્તિત્વ નથી
A (-1) I
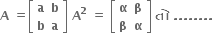
α= 2ab, β = a2 + b2
α= a2 + b2, β= ab
α= a2 + b2, β = a2 - b2
α= a2 + b2, β = 2ab
 અને જો B એ A નો વ્યસ્ત શ્રેણિક હોય તો α = ........
અને જો B એ A નો વ્યસ્ત શ્રેણિક હોય તો α = ........ -1
5
-1
-2
B.
5
Tips: -
અહીં B = A-1 આપેલ છે.
∴ AB = I
10(AB) = 10 I
∴ A(10 B) = 10 I

∴ α + 5 = 10
∴ α = 5 ( α = 5 તો 5 - α = α- 5 = 0)
જો 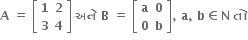
અસિમિત સંખ્યામાં B મળે કે જેથી AB = BA
એક B મળે કે જેથી AB = BA
એક કરતાં વધુ પરંતુ સિમિત સંખ્યામાં B મળે જે જેથી AB = BA
AB = BA થાય, તેવો B મળે નહિ
ધારો કે A એ 2 × 2 શ્રેણિક છે, I એ 2 × 2 એકમ શ્રેણિક છે. શ્રેણિકના વિકર્ણના ઘટકોના સરવાળાને tr (A) વડે દર્શાવીએ તથા A2 = I
વિધાન 1 : જો A # I અને A # -I તો  = -1
= -1
વિધાન 2 : જો A # I અને A # I તો tr(A) # 0
વિધાન 1 સત્ય છે; વિધાન 2 એ સત્ય છે. વિધાન 2 એ વિધાન 1 ની સાચી સમજૂતી આપે છે.
વિધાન 1 સત્ય છે તથા વિધાન 2 સત્ય છે. વિધાન 2 એ વિધાન 1 ની સાચી સમજૂતી નથી.
વિધાન 1 સત્ય છે તથા વિધાન 2 અસત્ય છે.
વિધાન 1 અસત્ય છે તથા વિધાન 2 સત્ય છે.
જો 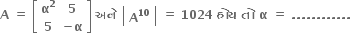
-2
2
3
-3
ધારો કે A એ 2×2 શ્રેણિક છે.
વિધાન 1 : adj (adj A) = A
વિધાન 2 : adj A = A
વિધાન 1 સત્ય છે; વિધાન 2 એ સત્ય છે. વિધાન 2 એ વિધાન 1 ની સાચી સમજૂતી આપે છે.
વિધાન 1 સત્ય છે તથા વિધાન 2 સત્ય છે. વિધાન 2 એ વિધાન 1 ની સાચી સમજૂતી નથી.
વિધાન 1 સત્ય છે તથા વિધાન 2 અસત્ય છે.
વિધાન 1 અસત્ય છે તથા વિધાન 2 સત્ય છે.
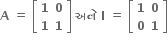 તો ગણિતિય અનુમાનના સિદ્ધાંતથી નીચેના પૈકી કયું સત્ય છે ? (n ≥ 1)
તો ગણિતિય અનુમાનના સિદ્ધાંતથી નીચેના પૈકી કયું સત્ય છે ? (n ≥ 1)An = nA + (n-1)I
An - nA - (n-1)I
An = 2n-1 A-(n-1)I
An = 2n-1 = nA + (n -1)I
AB=BA
A અથવા B શુન્ય શ્રેણિક છે.
A = B
A અથવા B એકમ શ્રેણિક છે.