CBSE
 Multiple Choice Questions
Multiple Choice Questionsવિધાન 1 સત્ય છે; વિધાન 2 એ સત્ય છે. વિધાન 2 એ વિધાન 1 ની સાચી સમજૂતી આપે છે.
વિધાન 1 સત્ય છે તથા વિધાન 2 સત્ય છે. વિધાન 2 એ વિધાન 1 ની સાચી સમજૂતી નથી.
વિધાન 1 સત્ય છે તથા વિધાન 2 અસત્ય છે.
વિધાન 1 અસત્ય છે તથા વિધાન 2 સત્ય છે.
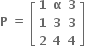 એ 3×3 શ્રેણિક Aનો સહાવયવ શ્રેણિક હોય અને = 4 તો α = .....
એ 3×3 શ્રેણિક Aનો સહાવયવ શ્રેણિક હોય અને = 4 તો α = .....
0
4
5
11
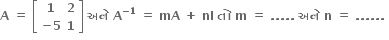
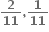
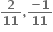
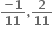
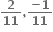
જો 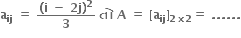
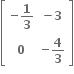
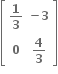
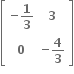

ધારો કે A એ શુન્યેતર ઘટકો વાળો 2 × 2 શ્રેણિક છે. અને A2 = I;I એ 2 × 2 એકમ શ્રેણિક છે.
ધારો કે tr(A) = A ના વિકર્ણના ઘટકોનો સરવાળો અને = det A
વિધાન 1 : tr (A) = 0
વિધાન 2 : = - 1
વિધાન 1 સત્ય છે; વિધાન 2 એ સત્ય છે. વિધાન 2 એ વિધાન 1 ની સાચી સમજૂતી આપે છે.
વિધાન 1 સત્ય છે તથા વિધાન 2 સત્ય છે. વિધાન 2 એ વિધાન 1 ની સાચી સમજૂતી નથી.
વિધાન 1 સત્ય છે તથા વિધાન 2 અસત્ય છે.
વિધાન 1 અસત્ય છે તથા વિધાન 2 સત્ય છે.
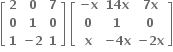 એકમ શ્રેણિક થાય ?
એકમ શ્રેણિક થાય ?
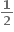
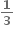

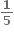
34, -19
-34, 19
-34, -19
34,19

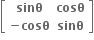
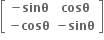
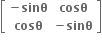
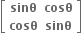
ધારો કે A અને B એ 3×3 સંમિત શ્રમિકો છે.
વિધાન 1 : A(BA) અને (AB)A સંમિત શ્રેણિકો છે.
વિધાન 2 : જો A નો B સાથે શ્રેણિકોનો ગુણાકાર ક્રમના નિયમોનું પાલન કરે તો AB સંમિત છે.
વિધાન 1 સત્ય છે; વિધાન 2 એ સત્ય છે. વિધાન 2 એ વિધાન 1 ની સાચી સમજૂતી આપે છે.
વિધાન 1 સત્ય છે તથા વિધાન 2 સત્ય છે. વિધાન 2 એ વિધાન 1 ની સાચી સમજૂતી નથી.
વિધાન 1 સત્ય છે તથા વિધાન 2 અસત્ય છે.
વિધાન 1 અસત્ય છે તથા વિધાન 2 સત્ય છે.
B.
વિધાન 1 સત્ય છે તથા વિધાન 2 સત્ય છે. વિધાન 2 એ વિધાન 1 ની સાચી સમજૂતી નથી.
Tips: -
A અને B સંમિત શ્રેણિક હોવાથી, AT = A, BT = B
[A(BA)]T = (BA)TAT
=(ATBT) AT
(AB) A = A(BA)
તે જ રીતે [(AB)A]T = (AB)A
A(BA) અને (AB) A સંમિત શ્રેણિક છે.
વિધાન 1 સત્ય છે.
જો AB = BA તો (AB)T = BTAT = BA + AB આથી AB સંમિત શ્રેણિક છે.
વિધાન 2 સત્ય છે.
પરંતુ વિધાન 2 અને વિધાન 1 ની સાચી સમજૂતી નથી.
વિધાન 1 : 3×3 વિસંમત શ્રેણિકોનો નિશ્ચાયક શુન્ય છે.
વિધાન 2 : કોઈ પણ શ્રેણિક A માટે 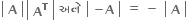
વિધાન 1 સત્ય છે; વિધાન 2 એ સત્ય છે. વિધાન 2 એ વિધાન 1 ની સાચી સમજૂતી આપે છે.
વિધાન 1 સત્ય છે તથા વિધાન 2 સત્ય છે. વિધાન 2 એ વિધાન 1 ની સાચી સમજૂતી નથી.
વિધાન 1 સત્ય છે તથા વિધાન 2 અસત્ય છે.
વિધાન 1 અસત્ય છે તથા વિધાન 2 સત્ય છે.