Book Store

Download books and chapters from book store.
Currently only available for.
CBSE

Gujarati JEE Mathematics : સંકર સંખ્યાઓ

Multiple Choice Questions

1. જો ચતુર્ઘાત સમીકરણ x⁴ + ax³ + bx² + cx + d = 0 (a, b, c, d ∈ R) નું કોઈપણ બીજ વાસ્તવિક સંખ્યા ન હોય તથા બે બીજનો સરવાળો 3 + 4 $bold i with bold hat on top$ હોય અને બાકીનાં બે બીજનો ગુણાકાર 13 + i હોય, તો b = ......... .

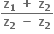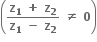
z₁ અને z₂ ભિન્ન સંકર સંખ્યાઓ છે તથા |z₁| = |z₂|. જો z₁ નો વાસ્તવિક ભાગ ધન સંખ્યા હોય તથા z₂ નો કાલ્પનિક ભાગ ઋણ સંખ્યા હોય, તો $fraction numerator bold z subscript bold 1 bold space bold plus bold space bold z subscript bold 2 over denominator bold z subscript bold 2 bold space bold minus bold space bold z subscript bold 2 end fraction$ એ ...... છે. $open parentheses fraction numerator bold z subscript bold 1 bold space bold plus bold space bold z subscript bold 2 over denominator bold z subscript bold 1 bold space bold minus bold space bold z subscript bold 2 end fraction bold space bold not equal to bold space bold 0 close parentheses$

વાસ્તવિક અને ધન
શુદ્વ કાલ્પનિક સંખ્યા
વાસ્તવિક અને ઋણ
શૂન્ય સંખ્યા

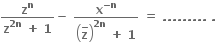
3. જો |z| = 1 અને z²ⁿ + 1 ≠ 0 તો $fraction numerator bold z to the power of bold n over denominator bold z to the power of bold 2 bold n end exponent bold space bold plus bold space bold 1 end fraction bold minus bold space fraction numerator bold x to the power of bold minus bold n end exponent over denominator open parentheses begin display style bold z with bold minus on top end style close parentheses to the power of bold 2 bold n end exponent bold space bold plus bold space bold 1 end fraction bold space bold equals bold space bold. bold. bold. bold. bold. bold. bold. bold. bold. bold space bold.$

4. જો α, β એ x²-2x + 2 = 0 નાં બીજ હોય, તો αⁿ + βⁿ = ......... .

$bold 2 to the power of begin inline style bold n over bold 2 end style end exponent bold space bold cos bold nπ over bold 4$
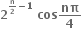
$bold 2 to the power of begin inline style bold n over bold 2 end style bold minus bold 1 end exponent bold space bold cos bold nπ over bold 4$
0
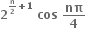
$bold 2 to the power of begin inline style bold n over bold 2 end style bold plus bold 1 end exponent bold space bold cos bold space bold nπ over bold 4$

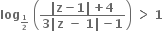$bold log subscript begin inline style bold 1 over bold 2 end style end subscript bold space open parentheses fraction numerator bold vertical line bold z bold minus bold 1 bold vertical line bold plus bold 4 over denominator bold 3 bold vertical line bold z bold space bold minus bold space bold 1 bold vertical line bold minus bold 1 end fraction close parentheses bold space bold greater than bold space bold 1$ (જ્યાં $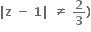bold vertical line bold z bold space bold minus bold space bold 1 bold vertical line bold space bold not equal to bold space bold 2 over bold 3 bold right parenthesis$ અસમતાનું પાલન કરતી સંકર સંખ્યાનો બિંદુગણ ......

વર્તુળનો બહારનો ભાગ.
વર્તુળ છે.
વર્તુળની અંદરનો ભાગ.
રેખા છે.

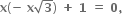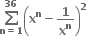6. જો $bold x open parentheses bold minus bold space bold x square root of bold 3 close parentheses bold space bold plus bold space bold 1 bold space bold equals bold space bold 0 bold comma bold space$ તો $bold sum from bold n bold equals bold 1 to bold 36 of open parentheses bold x to the power of bold n bold minus bold 1 over bold x to the power of bold n close parentheses to the power of bold 2$ = ........... .

7. જો x² + x + 1 = 0 નાં બે બીજ a અને b હોય, તો જેનાં બીજ a¹⁹ અને b⁷ હોય, તેવું સમીકરણ = .........

x² + x + 1 = 0
x² + x - 1 = 0
x² - x - 1 = 0
x² - x + 1 = 0

f(z)ને z-i વડે ભાગીએ તો શેષ i મળે છે તથા જો z + i વડે ભાગીએ તો શેષ 1 + i મળે છે. જો f(z) ને z² + 1 વડે ભાંગીએ તો મળતી શેષ ......

0
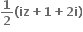
$bold 1 over bold 2 bold left parenthesis bold iz bold plus bold 1 bold plus bold 2 bold i bold right parenthesis$
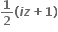
$bold 1 over bold 2 bold left parenthesis bold italic i bold italic z bold plus bold 1 bold right parenthesis$
iz+1+i

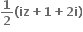
bold 1 over bold 2 bold left parenthesis bold iz bold plus bold 1 bold plus bold 2 bold i bold right parenthesis

Tips: -

f(z) ને z - iવડે ભાગીએ તો શેષ i મળે છે.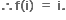

$bold therefore bold f bold left parenthesis bold i bold right parenthesis bold space bold equals bold space bold i bold.$ ... (1)

તે જ રીતે, f(-i) = 1 + i ... (2)

z² + 1 એ દ્વિઘાત પદાવલિ છે. તેથી f(z) ને z² + 1 વડે ભાગીએ, તો az + b (a, b ∈ R) પ્રકારની શેષ મળે.

ધારો કે, f(z) = g(z) (z² + 1) ai + b ... (3)

∴ f(i) = g(i) (i² + 1) + ai + b

∴ i = ai + b ... (4)

તથા f(-i) = g(-i)((-1)² + 1) + a(-i) + b

1 + i = - ai + b ... (5)

(4) અને (5) ને ઉકેલતાં, 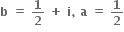$bold b bold space bold equals bold space bold 1 over bold 2 bold space bold plus bold space bold i bold comma bold space bold a bold space bold equals bold space bold 1 over bold 2$

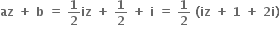
$bold therefore$ માંગલે શેષ $bold az bold space bold plus bold space bold b bold space bold equals bold space bold 1 over bold 2 bold iz bold space bold plus bold space bold 1 over bold 2 bold space bold plus bold space bold i bold space bold equals bold space bold 1 over bold 2 bold space bold left parenthesis bold iz bold space bold plus bold space bold 1 bold space bold plus bold space bold 2 bold i bold right parenthesis$

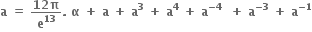ધારો કે $bold a bold space bold equals bold space fraction numerator bold 12 bold pi over denominator bold e to the power of bold 13 end fraction bold. bold space bold alpha bold space bold plus bold space bold a bold space bold plus bold space bold a to the power of bold 3 bold space bold plus bold space bold a to the power of bold 4 bold space bold plus bold space bold a to the power of bold minus bold 4 end exponent bold space bold space bold plus bold space bold a to the power of bold minus bold 3 end exponent bold space bold plus bold space bold a to the power of bold minus bold 1 end exponent$ તથા $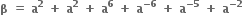bold beta bold space bold equals bold space bold a to the power of bold 2 bold space bold plus bold space bold a to the power of bold 2 bold space bold plus bold space bold a to the power of bold 6 bold space bold plus bold space bold a to the power of bold minus bold 6 end exponent bold space bold plus bold space bold a to the power of bold minus bold 5 end exponent bold space bold plus bold space bold a to the power of bold minus bold 2 end exponent$ જેનાં બીજ હોય તેવું દ્વિઘાત સમીકરણ ......... છે.

x² + x + 3 = 0
x² - x + 2 = 0
x² + x - 3 = 0
x³ - x - 3 = 0

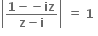10. જો, $open vertical bar fraction numerator bold 1 bold minus bold minus bold iz over denominator bold z bold minus bold i end fraction close vertical bar bold space bold equals bold space bold 1 bold space$ તો.......

z એ શુદ્વ કાલ્પનિક સંખ્યા હોય.
P(z) એ બીજા ચરણમાં હોય.
P(z) એ ત્રીજા ચરણમાં હોય.
z એ વાસ્તવિક સંખ્યા હોય.

Switch

Book Store

Subject

Gujarati JEE Mathematics : સંકર સંખ્યાઓ

Multiple Choice Questions

Switch